5.3.1 Arithmetic Progressions, SPM Practice (Paper 1)

Question 1:
The third and eighth terms of an arithmetic progression are –5 and 15 respectively. Find
(a) The first term and the common difference
(b) The sum of the first 10 terms.

Solution:
(a)
$\begin{array}{l}{T}_3=-5\to \text{ Use }{T}_n=a+\left(n-1\right)d\\ a+2d=-5\to \left(1\right)\\ T_8=15\\ a+7d=15\to \left(2\right)\\ \\ \left(2\right)-\left(1\right),\\ 5d=20\\ d=4\\ \text{Substitute }d=4\text{ into }\left(1\right),\\ a+2\left(4\right)=-5\\ a=-13\end{array}$

(b)
$\begin{array}{l}{S}_{10}=\frac{10}{2}\left[2\left(-13\right)+9\left(4\right)\right]\to \text{Use }{S}_n=\frac{n}{2}\left[2a+\left(n-1\right)d\right]\\ =50\end{array}$

Question 2:
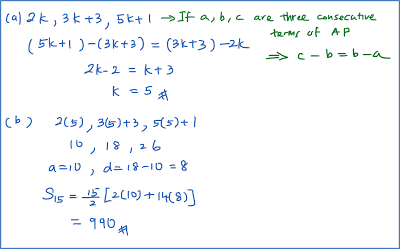
The first three terms of an arithmetic progression are 2k, 3k + 3, 5k + 1. Find
(a) the value of k,
(b) the sum of the first 15 terms of the progression.

Solution:

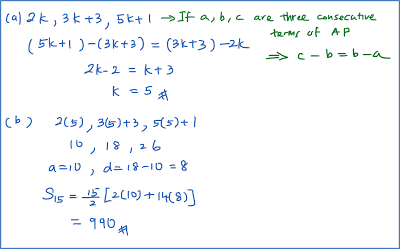
Question 3:
Given an arithmetic progression p + 9, 2p + 10, 7p – 1,… where p is a constant. Find
(a) value of p,
(b) the sum of the next five terms.

Solution:

Question 4:
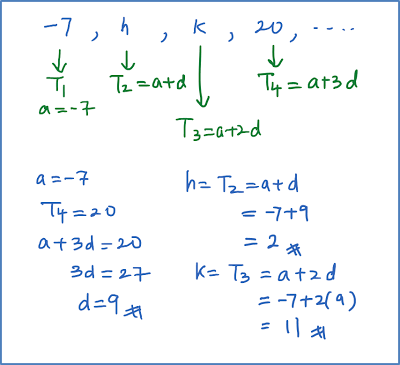
It is given that -7, h, k, 20,… are the first four terms of an arithmetic progression. Find the value of h and of k.

Solution:

Question 5:
51, 58, 65,… 191 are the first n terms of an arithmetic progression. Find the value of n.

Solution: