5.3.2 Arithmetic Progressions, SPM Practice (Paper 1)

Question 6:
Find the number of the multiples of 8 between 100 and 300.

Solution:

Question 7:
Find the sum of all the multiples of 7 between 100 and 500.

Solution:

Question 8:
If ${\log }_{10}p,{\log }_{10}pq\text{ and }{\log }_{10}p{q}^2$ are the first three terms of a progression, show that it forms an arithmetic progression.

Solution:

Question 9:


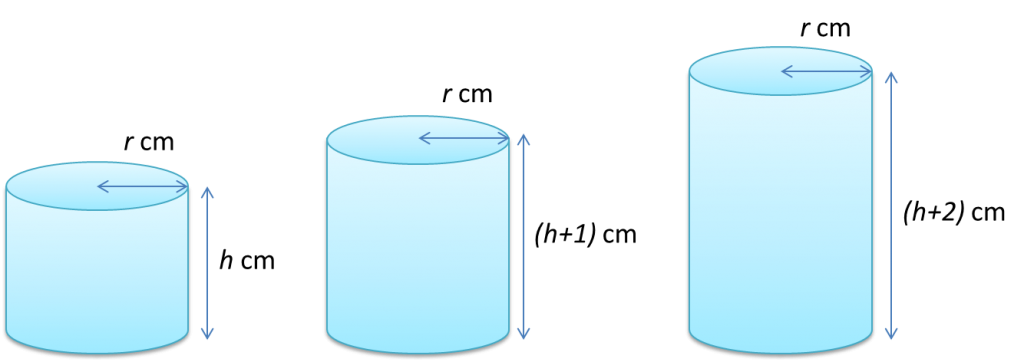
Show that the volumes of the cylinders in the above diagram form an arithmetic progression and state its common difference.

Solution:

Question 10:
The sequence –11, –5, 1,… is an arithmetic progression. State the three consecutive terms of this arithmetic progression where the sum of these three terms is 93.

Solution: