2.2 First Derivative for Polynomial Function
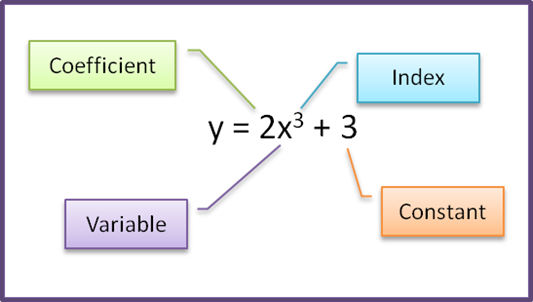
(A) Differentiating a Constant
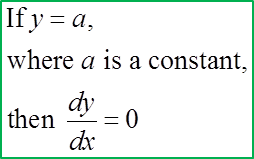
(B) Differentiating Variable with Index n
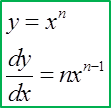
(C) Differentiating a Linear Function
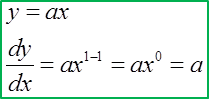
(D) Differentiating a Polynomial Function
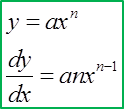
(E) Differentiating Fractional Function
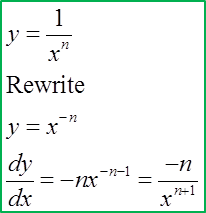
(F) Differentiating Square Root Function
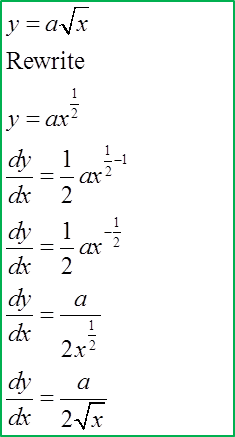

(A) Differentiating a Constant
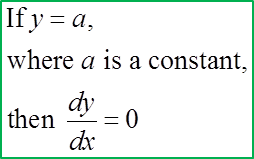
(B) Differentiating Variable with Index n
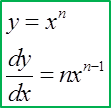
(C) Differentiating a Linear Function
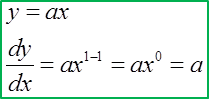
(D) Differentiating a Polynomial Function
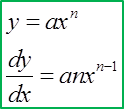
(E) Differentiating Fractional Function
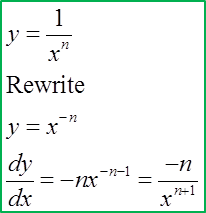
(F) Differentiating Square Root Function
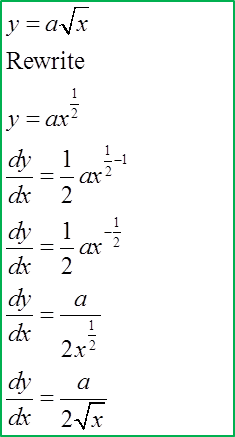
Example:
Find
for each of the following functions:
(a) y= 12
(b) y= x4
(c) y= 3x
(d) y= 5x3
Solution:
(a)
y = 12
y = 12
(b)
y = x4
y = x4
= 4x3
(c)
y = 3x
= 3
y = 5x3
= 3(5x2) = 15x2
(e)
(f)
(g)
(h)
(i)