Question 11 (SPM 2017 – 3 marks):
Diagram 5 shows the graph of the function f : x → |1 – 2x| for the domain –2 ≤ x ≤ 4.
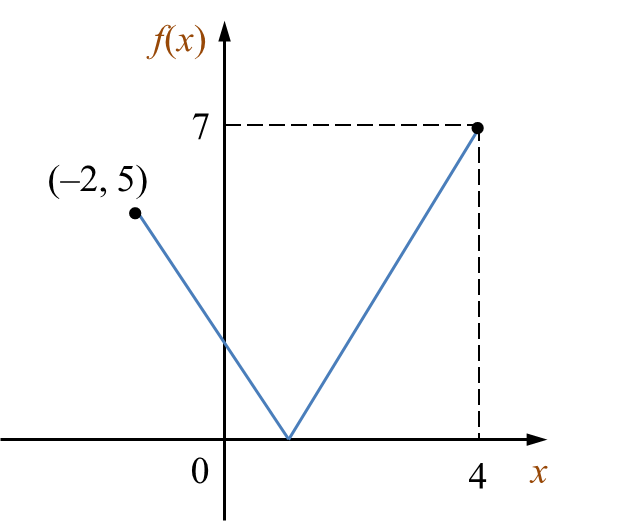 Diagram 5
Diagram 5
State
(a) the object of 7,
(b) the image of 3,
(c) the domain of 0 ≤ f(x) ≤ 5.
Solution:
(a)
The object of 7 is 4.
(b)
f (x) = |1 – 2x|
f (3) = |1 – 2(3)|
= |1 – 6|
= |–5|
= 5
The image of 3 is 5.
(c)
|1 – 2x| = 5
1 – 2x = ±5
Given when f(x) = 5, x = –2.
When f(x) = –5
1 – 2x = –5
2x = 6
x = 3
Domain: –2 ≤ x ≤ 3.
Diagram 5 shows the graph of the function f : x → |1 – 2x| for the domain –2 ≤ x ≤ 4.
 Diagram 5
Diagram 5 State
(a) the object of 7,
(b) the image of 3,
(c) the domain of 0 ≤ f(x) ≤ 5.
Solution:
(a)
The object of 7 is 4.
(b)
f (x) = |1 – 2x|
f (3) = |1 – 2(3)|
= |1 – 6|
= |–5|
= 5
The image of 3 is 5.
(c)
|1 – 2x| = 5
1 – 2x = ±5
Given when f(x) = 5, x = –2.
When f(x) = –5
1 – 2x = –5
2x = 6
x = 3
Domain: –2 ≤ x ≤ 3.
Question 12 (SPM 2017 – 4 marks):
Given the function g : x → 2x – 8, find
Solution:
(a)
(b)
Given the function g : x → 2x – 8, find
Solution:
(a)
(b)
Question 13 (SPM 2018 – 4 marks):
Diagram 9 shows the relation between set A, set B and set C.
 Diagram 9
Diagram 9
It is given that set A maps to set B by the function and maps to set C by fg : x → x2 + 2x + 4.
(a) Write the function which maps set A to set B by using the function notation.
(b) Find the function which maps set B to set C.
Solution:
 (a)
(a)
(b)
Diagram 9 shows the relation between set A, set B and set C.
 Diagram 9
Diagram 9It is given that set A maps to set B by the function and maps to set C by fg : x → x2 + 2x + 4.
(a) Write the function which maps set A to set B by using the function notation.
(b) Find the function which maps set B to set C.
Solution:
 (a)
(a)(b)
Question 14:
Solution:
Solution:
Question 15 (SPM 2019):
Diagram 2 shows the relation of three sets.
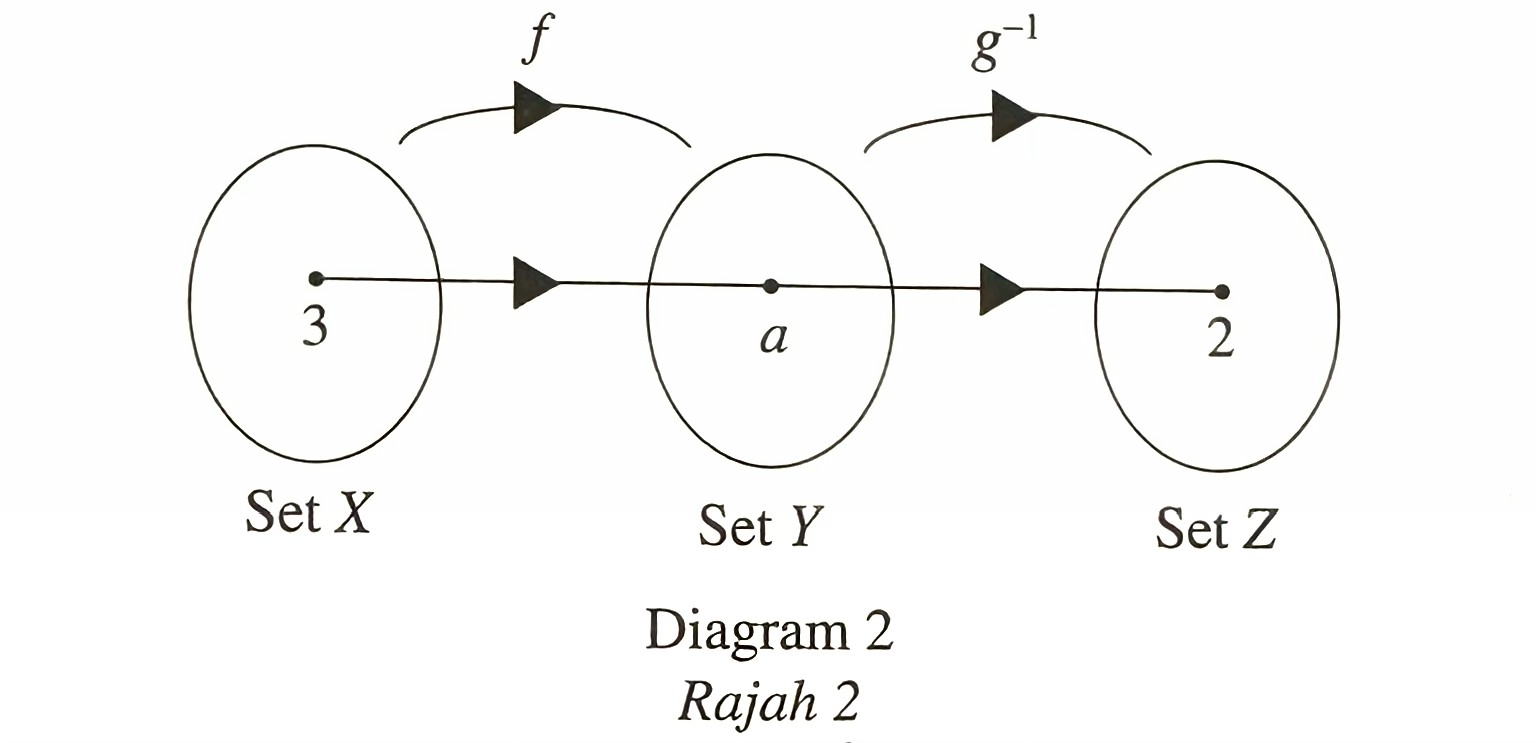
$$ \text { It is given that } f: x \rightarrow 2 x+3 \text { and } g^{-1} f: x \rightarrow \frac{3}{x}+1, x \neq 0 \text {. } $$
(a) If a student writes a = 10, determine whether the value is correct or wrong. Give your reason.
(b) Find g-1(x).
[4 marks]
Answer:
(a)
$$ \begin{aligned} &\begin{aligned} & f(x)=2 x+3 \\ & f(3)=2(3)+3=9 \\ & f(3)=a=9 \end{aligned}\\ &\text { The value of } a=10 \text { is wrong. } \end{aligned} $$
(b)
$$ \begin{aligned} & g^{-1} f(x)=\frac{3}{x}+1 \\ & g^{-1}(2 x+3)=\frac{3}{x}+1 \\ & \text { Let } 2 x+3=u \\ & 2 x=u-3 \\ & x=\frac{u-3}{2} \\ & g^{-1}(u)=\frac{\frac{3}{u-3}}{2}+1 \\ & =\frac{6}{u-3}+1 \\ & g^{-1}(x)=\frac{6}{x-3}+1, x \neq 3 \end{aligned} $$
Diagram 2 shows the relation of three sets.

$$ \text { It is given that } f: x \rightarrow 2 x+3 \text { and } g^{-1} f: x \rightarrow \frac{3}{x}+1, x \neq 0 \text {. } $$
(a) If a student writes a = 10, determine whether the value is correct or wrong. Give your reason.
(b) Find g-1(x).
[4 marks]
Answer:
(a)
$$ \begin{aligned} &\begin{aligned} & f(x)=2 x+3 \\ & f(3)=2(3)+3=9 \\ & f(3)=a=9 \end{aligned}\\ &\text { The value of } a=10 \text { is wrong. } \end{aligned} $$
(b)
$$ \begin{aligned} & g^{-1} f(x)=\frac{3}{x}+1 \\ & g^{-1}(2 x+3)=\frac{3}{x}+1 \\ & \text { Let } 2 x+3=u \\ & 2 x=u-3 \\ & x=\frac{u-3}{2} \\ & g^{-1}(u)=\frac{\frac{3}{u-3}}{2}+1 \\ & =\frac{6}{u-3}+1 \\ & g^{-1}(x)=\frac{6}{x-3}+1, x \neq 3 \end{aligned} $$