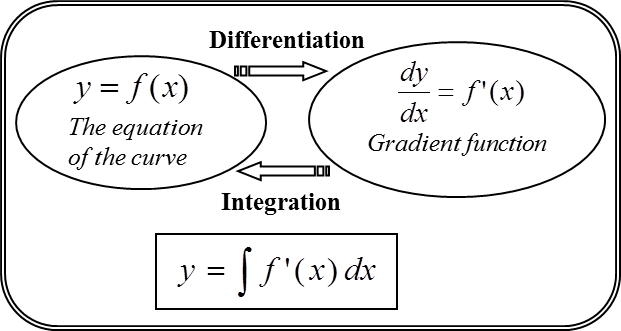
3.3 Finding Equation of a Curve from its Gradient Function
Example 1:
Find the equation of the curve that has the gradient function and passes through the point (2, 3).
Solution:
Find the equation of the curve that has the gradient function and passes through the point (2, 3).
Solution:
y = x2 + 8x + C
3 = 22 +8(2) + C (2, 3)
C = –17
Hence, the equation of the curve is
y = x2 + 8x – 17
Hence, the equation of the curve is
y = x2 + 8x – 17
Example 2:
The gradient function of a curve is given by 2x – 4 and the curve has a minimum value of 3. Find the equation of the curve.
Solution:
At the point where a curve has a minimum value,
2x – 4 = 0
x = 2
Therefore minimum point = (2, 3).
When x = 2, y = 3.
3 = 22 – 4(2) + c
c = 7
Hence, the equation of the curve is
y = x2 – 4x + 7