Question 1:
Diagram below shows the relation between set M and set N in the graph form.
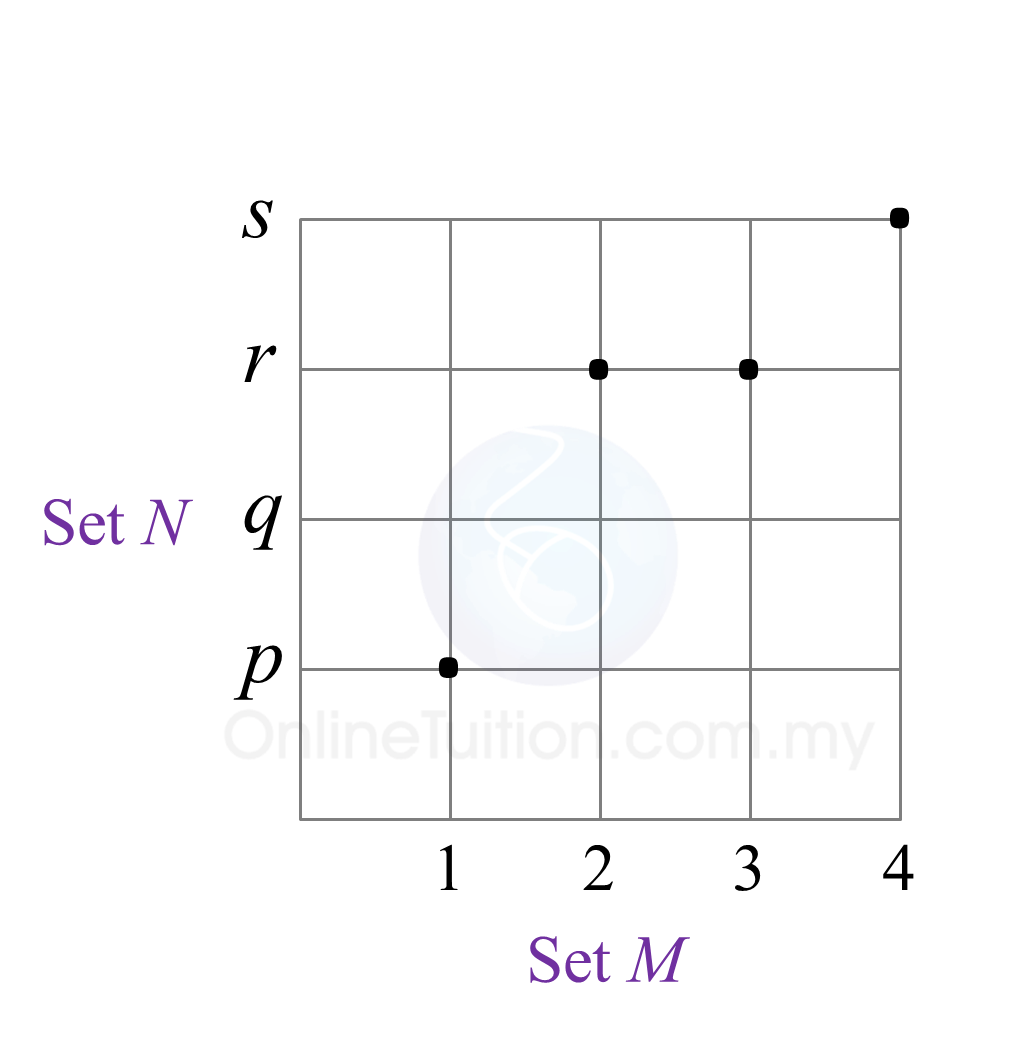 State
State
(a) the range of the relation,
(b) the type of the relation between set M and set N.
Solution:
(a) Range of the relation = {p, r, s}.
(b) Type of the relation between set M and set N is many to one relation.
Diagram below shows the relation between set M and set N in the graph form.
 State
State(a) the range of the relation,
(b) the type of the relation between set M and set N.
Solution:
(a) Range of the relation = {p, r, s}.
(b) Type of the relation between set M and set N is many to one relation.
Question 2:
Diagram below shows the relation between set P and set Q.

State
(a) the object of 3,
(b) the range of the relation.
Solution:
(a) The object of 3 is 7.
(b) The range of the relation is {–3, –1, 1, 3}.
Diagram below shows the relation between set P and set Q.

State
(a) the object of 3,
(b) the range of the relation.
Solution:
(a) The object of 3 is 7.
(b) The range of the relation is {–3, –1, 1, 3}.
Question 3:
Diagram below shows the function g : x → x – 2k, where k is a constant.
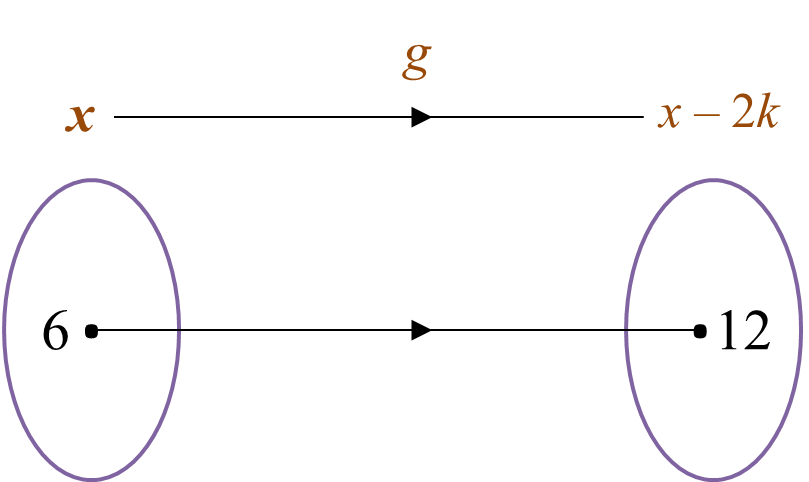
Find the value of k.
Solution:
Diagram below shows the function g : x → x – 2k, where k is a constant.

Find the value of k.
Solution:
Question 4:
Diagram below shows the relation between set M and set N in the arrow diagram.
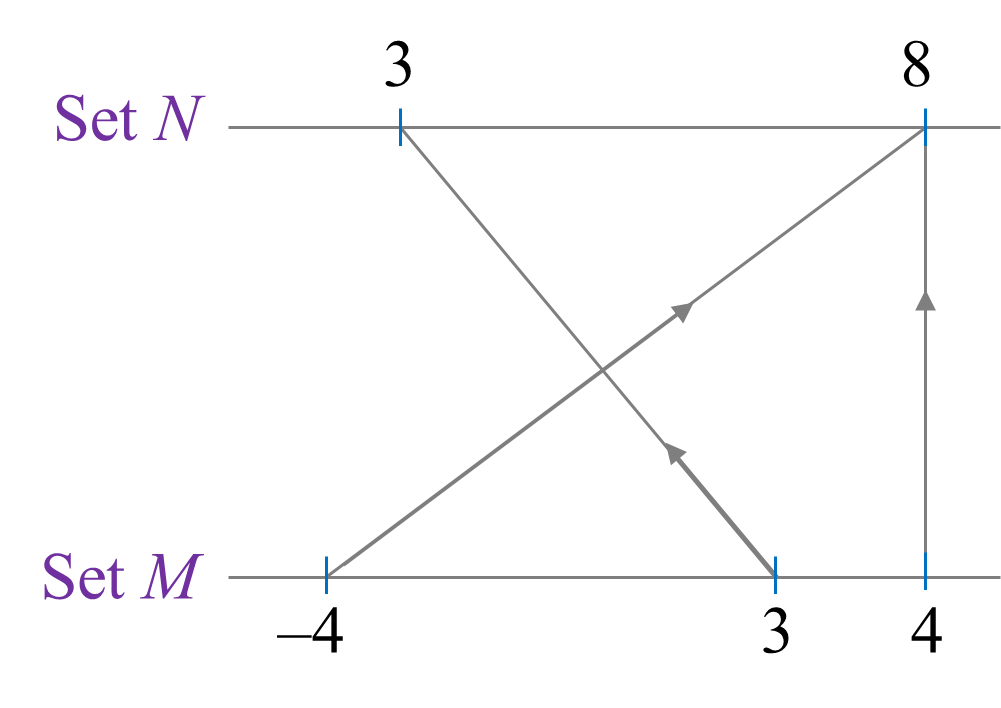
(a) Represent the relation in the form of ordered pairs.
(b) State the domain of the relation.
Solution:
(a) Relation in the form of ordered pairs = {(–4, 8), (3, 3), (4, 8)}.
(b) Domain of the relation = {–4, 3, 4}.
Diagram below shows the relation between set M and set N in the arrow diagram.

(a) Represent the relation in the form of ordered pairs.
(b) State the domain of the relation.
Solution:
(a) Relation in the form of ordered pairs = {(–4, 8), (3, 3), (4, 8)}.
(b) Domain of the relation = {–4, 3, 4}.
Question 5:
It is given the functions g(x) = 3x and h(x) = m – nx, where m and n are constants.
Express m in terms of n such that hg(1) = 4.
Solution:
It is given the functions g(x) = 3x and h(x) = m – nx, where m and n are constants.
Express m in terms of n such that hg(1) = 4.
Solution:
Question 6:
Given the function g : x → 3x – 2, find
(a) the value of x when g(x) maps onto itself,
(b) the value of k such that g(2 – k) = 4k.
Solution:
(a)
(b)
Given the function g : x → 3x – 2, find
(a) the value of x when g(x) maps onto itself,
(b) the value of k such that g(2 – k) = 4k.
Solution:
(a)
(b)
Question 7:
Given the functions f : x → px + 1, g : x → 3x – 5 and fg(x) = 3px + q.
Express p in terms of q.
Solution:
Given the functions f : x → px + 1, g : x → 3x – 5 and fg(x) = 3px + q.
Express p in terms of q.
Solution:
Question 8:
Given the functions h : x → 3x + 1, and gh : x → 9x2 + 6x – 4, find
(a) h-1 (x),
(b) g(x).
Solution:
(a)
(b)
Given the functions h : x → 3x + 1, and gh : x → 9x2 + 6x – 4, find
(a) h-1 (x),
(b) g(x).
Solution:
(a)