Question 4 (3 marks):
Diagram 4 shows a trapezium ABCD.
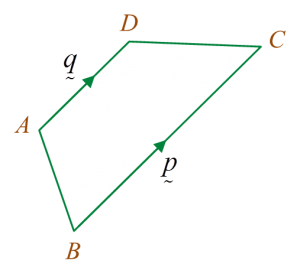 Diagram 4
Diagram 4
Solution:
Diagram 4 shows a trapezium ABCD.
 Diagram 4
Diagram 4Solution:
Question 5 (3 marks):
Solution:
Solution:
Question 6 (3 marks):
Solution:
Solution:
Question 7 (2 marks):
It is given that the nth term of a geometric progression is
State
(a) the value of k,
(b) the first term of progression.
Solution:
(a)
k = 0, k = 1 or k = -1 (Any one of these answer).
(b)
It is given that the nth term of a geometric progression is
State
(a) the value of k,
(b) the first term of progression.
Solution:
(a)
k = 0, k = 1 or k = -1 (Any one of these answer).
(b)