9.4.5 Solution of Triangles, Long Questions (Question 9)

Question 9

Diagram 6 shows a quadrilateral KLMN.

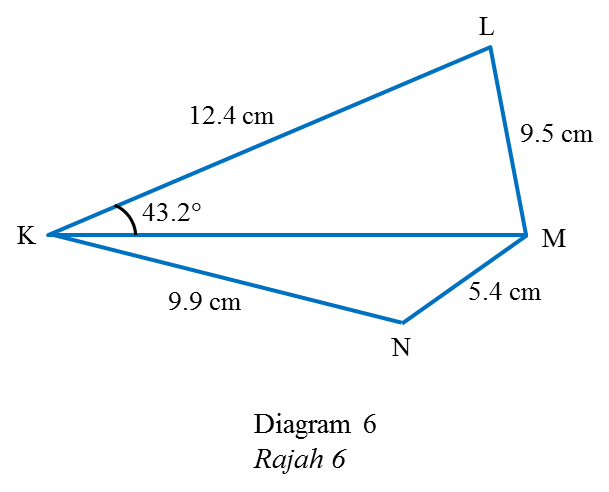
Calculate

(a) ∠KML, [2 marks]

(b) the length, in cm, of KM, [3 marks]

(c) area, in cm², of triangle KMN, [3 marks]

(d) a triangle K’L’M’ has the same measurements as those given for triangle KLM, that is K’L’= 12.4 cm, L’M’= 9.5 cm and ∠L’K’M’= 43.2^o, which is different in shape to triangle KLM.
(i) Sketch the triangle K’L’M’,
(ii) State the size of ∠K’M’L’. [2 marks]

Solution:

(a)

\begin{array}{l} \frac{\sin ∠ K M L}{12.4} = \frac{\sin {43.2}^{o}}{9.5} \\ \sin ∠ K M L = \frac{\sin {43.2}^{o}}{9.5} \times 12.4 \\ \sin ∠ K M L = 0.8935 \\ ∠ K M L = {63.32}^{o} \end{array}

(b)

∠KLM = 180^o – 43.2^o – 63.32^o = 73.48^o

KM²= 9.5² + 12.4² – 2(9.5)(12.4) cos 73.48^o

KM²= 244.01 – 66.99

KM²= 177.02

KM= 13.30 cm

(c)

KM²= MN²+ KN²– 2(MN)(KN) cos ∠KNM

13.30²= 5.4² + 9.9²– 2(5.4)(9.9) cos ∠KNM

176.89 = 127.17 – 106.92 cos ∠KNM

\begin{array}{l} \cos ∠ K N M = \frac{127.17 - 176.89}{106.92} \\ ∠ K N M = {117.71}^{o} \end{array}

Area of triangle KMN

\begin{array}{l} = \frac{1}{2} (5.4) (9.9) \sin {117.71}^{o} \\ = 23.66 c m^{2} \end{array}

(d)(i)

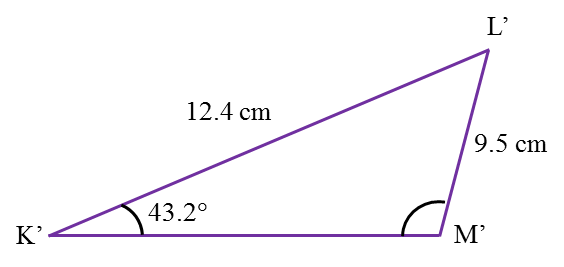
(d)(ii)

∠K’M’L’ = 180^o – 63.32^o= 116.68^o

Leave a Comment Cancel reply