8.3.2 Subtraction of Vectors
The subtraction of the vector
from the vector
is written as
. This operation can be considered as the addition of the vector
with the negative vector of
. Therefore
Example 1:
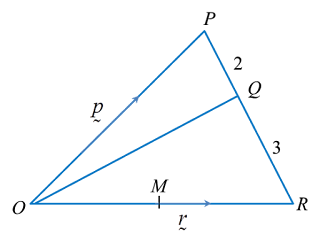
In the diagram above, vector and Q divides PR in the ratio of 2 : 3. Find the following vectors in terms of
Solution:
(a)
(b)
(c)