Question 5:
In Diagram below, the straight line WY is normal to the curve at B (2, 4). The straight line BQ is parallel to the y–axis.
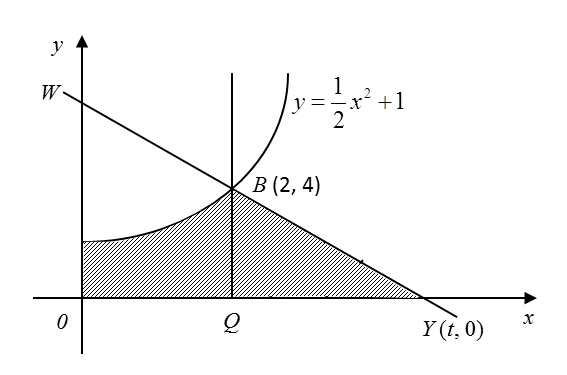
Find
(a) the value of t,
(b) the area of the shaded region,
(c) the volume generated, in terms of π, when the region bounded by the curve, the y–axis and the straight line y = 4 is revolved through 360° about the y-axis.
Solution:
(a)
(b)
(c)
In Diagram below, the straight line WY is normal to the curve at B (2, 4). The straight line BQ is parallel to the y–axis.

Find
(a) the value of t,
(b) the area of the shaded region,
(c) the volume generated, in terms of π, when the region bounded by the curve, the y–axis and the straight line y = 4 is revolved through 360° about the y-axis.
(a)
(b)
(c)
Question 6:
Diagram below shows part of the curve which passes through B (1, 2).
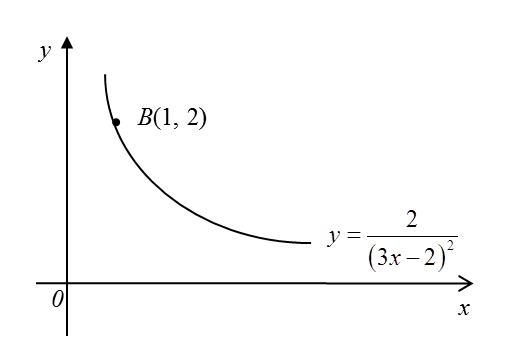
(a) Find the equation of the tangent to the curve at the point B.
(b) A region is bounded by the curve, the x-axis and the straight lines x = 2 and x = 3.
(i) Find the area of the region.
(ii) The region is revolved through 360° about the x–axis. Find the volume generated, in terms of p.
Solution:
(a)
(b)(i)
(b)(ii)
Diagram below shows part of the curve which passes through B (1, 2).

(a) Find the equation of the tangent to the curve at the point B.
(b) A region is bounded by the curve, the x-axis and the straight lines x = 2 and x = 3.
(i) Find the area of the region.
(ii) The region is revolved through 360° about the x–axis. Find the volume generated, in terms of p.
(a)
(b)(i)
(b)(ii)