Question 3:
The gradient function of a curve which passes through P(2, –14) is 6x² – 12x.
Find
(a) the equation of the curve,
(b) the coordinates of the turning points of the curve and determine whether each of the turning points is a maximum or a minimum.
Solution:
(a)
Given gradient function of a curve dydx=6x2−12xThe equation of the curve,y=∫(6x2−12x) dxy=6x33−12x22+cy=2x3−6x2+c−14=2(2)3−6(2)2+c, at point P (2,−14)−14=−8+cc=−6y=2x3−6x2−6
(b)
dydx=6x2−12xAt turning points, dydx=06x2−12x=06x(x−2)=0x=0, x=2x=0, y=2(0)3−6(0)2−6=−6x=2, y=2(2)3−6(2)2−6=−14d2ydx2=12x−12When x=0, d2ydx2=12(0)−12=−12 <0(0,−6) is a maximum point.When x=2, d2ydx2=12(2)−12=12 >0(2,−14) is a minimum point.
Question 4:
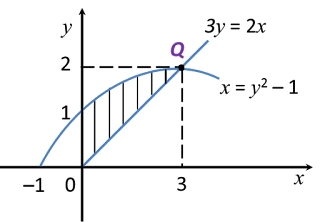
Diagram below shows a curve x = y2 – 1 which intersects the straight line 3y = 2x at point Q.
Calculate the volume generated when the shaded region is revolved 360o about the y-axis.
Solution:
x=y2−1→(1)3y=2xx=32y→(2)Substitute (2) into (1),32y=y2−12y2−3y−2=0(2y+1)(y−2)=0y=−12 or y=2
When y=2,x=32(2)=3, Q=(3, 2)I1(Volume of cone)=13πr2h=13π(3)2(2)=6π unit3I2(Volume of the curve)= π∫21x2dy= π∫21(y2−1)2dy= π∫21(y4−2y2+1)dy=π[y55−2y33+y]21=π[(255−2(2)33+2)−(155−2(1)33+1)]=π(4615−815)=3815π unit3∴ Volume generated =I1−I2 =6π−3815π =5215π unit3
