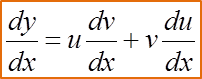2.3 Find the Derivatives of a Product using Product Rule
(A) The Product Rule
Method 1
If u(x) and v(x) are two functions of x and y = uv then
Method 2 (Differentiate Directly)

Example:
Solution:

Example:
Solution:
Practice 1:
Solution:
y = 4x3 (3x + 1)5
dy/dx
Given that y = 4x3 (3x + 1)5, find dy/dx.
Solution:
y = 4x3 (3x + 1)5
dy/dx
= 4x3. 5(3x + 1)4.3 + (3x + 1)5.12x2
= 60x3 (3x + 1)4 + 12x2 (3x + 1)5
= 12x2(3x + 1)4 [5x + (3x+ 1)]
= 12x2(3x + 1)4 (8x + 1)