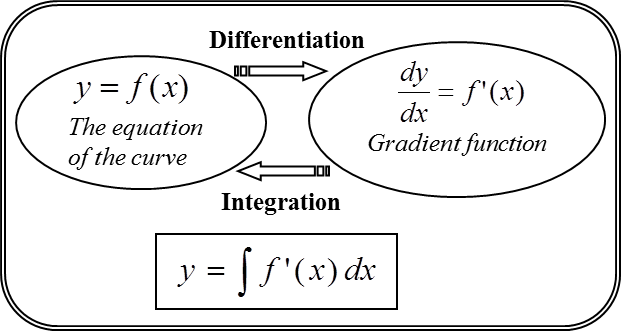
3.3 Finding Equation of a Curve from its Gradient Function

3.3 Finding Equation of a Curve from its Gradient Function

Example 1:
Find the equation of the curve that has the gradient function

$\frac{d y}{d x} = 2 x + 8$ and passes through the point (2, 3).

Solution:

$\begin{array}{l} y = \int (2 x + 8) \\ y = \frac{2 x^{2}}{2} + 8 x + C \end{array}$

y = x² + 8x + C

3 = 2² +8(2) + C (2, 3)

C = –17
Hence, the equation of the curve is
y = x² + 8x – 17

Example 2:

The gradient function of a curve is given by 2x – 4 and the curve has a minimum value of 3. Find the equation of the curve.

Solution:

At the point where a curve has a minimum value,

$\frac{d y}{d x} = 0$

2x – 4 = 0

x = 2

Therefore minimum point = (2, 3).

$\begin{array}{l} \frac{d y}{d x} = 2 x - 4 \\ y = \int (2 x - 4) d x \\ y = \frac{2 x^{2}}{2} - 4 x + C \\ y = x^{2} - 4 x + C \end{array}$

When x = 2, y = 3.

3 = 2² – 4(2) + c

c = 7

Hence, the equation of the curve is

y = x² – 4x + 7