Question 15:
Table 4 shows information for four ingredients used to produce a type of biscuit.
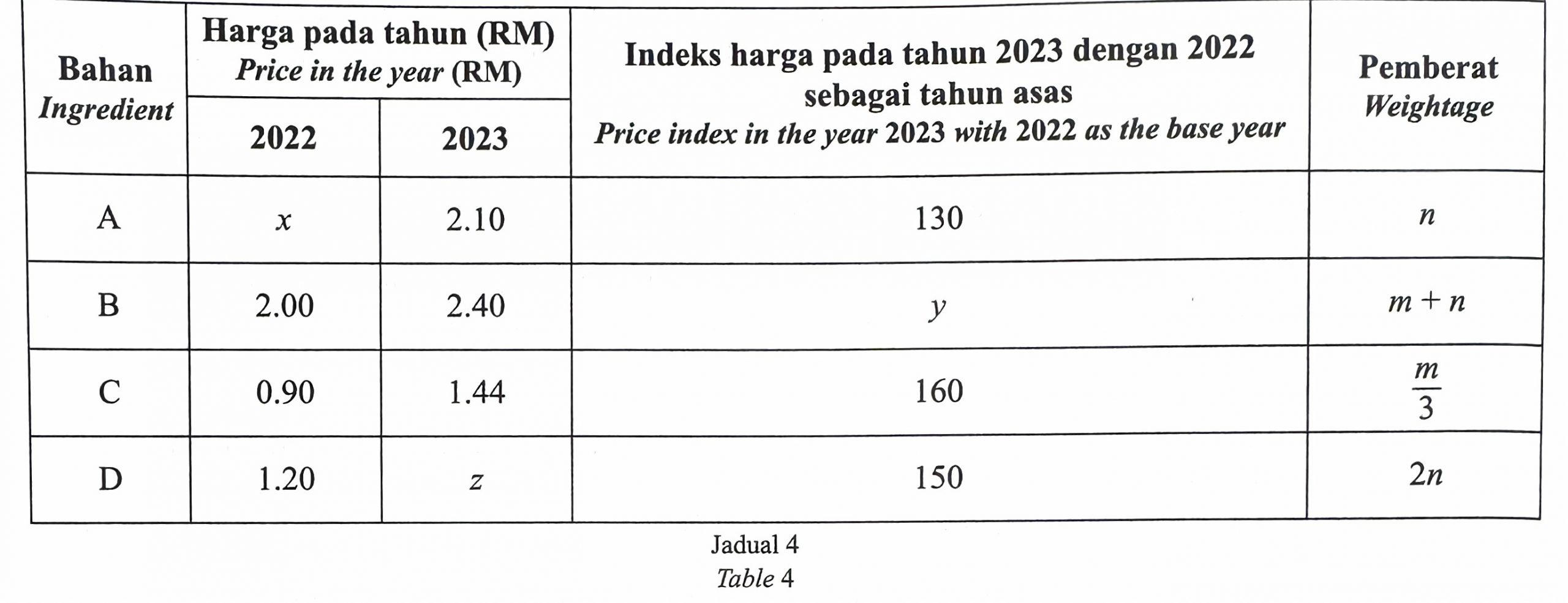
(a) Find the value of x, of y and of z.
[3 marks]
(b) The composite index for the production cost of the biscuit in the year 2023 with 2022 as the base year is 135.
(i) Find the ratio of ingredient A to ingredient B used.
(ii) The production cost of 200 biscuits in the year 2022 is RM25. The price of each ingredient is expected to increase by 20.25% from the year 2023 to the year 2025. In the year 2025, the box used to fit 40 biscuits is expected to cost RM1.50 per unit.
In the year 2025, if RM45 is allocated to produce 200 biscuits including the purchase of the box, determine whether or not the allocation is enough.
[7 marks]
Answer:
(a)
$$ \begin{aligned} \bar{I}_{\frac{23}{22}} & =130 \\ \frac{2.10}{x} \times 100 & =130 \\ \frac{2.10}{x} & =\frac{130}{100} \\ x & =\frac{2.10 \times 100}{130} \\ x & =1.62 \end{aligned} $$
$$ \begin{aligned} & y=\frac{2.40}{2.00} \times 100 \\ & y=120 \end{aligned} $$
$$ \begin{aligned} \bar{I}_{\frac{23}{22}} & =150 \\ \frac{z}{1.20} \times 100 & =150 \\ z & =\frac{150 \times 1.20}{100} \\ z & =1.80 \end{aligned} $$
(b)(i)
$$ \begin{aligned} \bar{I}_{\frac{23}{22}}=135 & \\ \frac{(130)(n)+(120)(m+n)+(160)\left(\frac{m}{3}\right)+(150)(2 n)}{n+m+n+\frac{m}{3}+2 n} & =135 \\ \frac{130 n+120 m+120 n+\frac{160}{3} m+300 n}{4 n+\frac{4}{3} m} & =135 \end{aligned} $$
$$ \begin{aligned} 550 n+\frac{520}{3} m & =135\left(4 n+\frac{4}{3} m\right) \\ 550 n+\frac{520}{3} m & =540 n+180 m \\ 550 n-540 n & =180 m-\frac{520}{3} m \\ 10 n & =\frac{20}{3} m \\ \frac{10}{\frac{20}{3}} & =\frac{m}{n} \\ \frac{3}{2} & =\frac{m}{n} \end{aligned} $$
$$ \therefore m: n=3: 2 $$
$$ \begin{aligned} & A: B=n: m+n \\ & A: B=2: 3+2 \\ & A: B=2: 5 \end{aligned} $$
(b)(ii)
$$ \begin{aligned} \bar{I}_{23 / 22} & =135 \\ \frac{P_{2023}}{P_{2022}} \times 100 & =135 \\ \frac{P_{2023}}{\mathrm{RM} 25} \times 100 & =135 \\ P_{2023} & =\frac{135 \times \mathrm{RM} 25}{100} \\ P_{2023} & =\mathrm{RM} 33.75 \end{aligned} $$
$$ \begin{aligned} \bar{I}_{25 / 23} & =100+20.25 \\ \frac{P_{2025}}{P_{2023}} \times 100 & =120.25 \\ \frac{P_{2025}}{\text { RM33.75 }} \times 100 & =120.25 \\ P_{2025} & =\frac{120.25 \times \text { RM33.75 }}{100} \\ P_{2025} & =\text { RM40.58 } \end{aligned} $$
$$ \begin{aligned} \text { Number of box } & =200 \div 40 \\ & =5 \end{aligned} $$
$$ \begin{aligned} \text { Price of box } & =5 \times \text { RM1.50 } \\ & =\text { RM7.50 } \end{aligned} $$
$$ \begin{aligned} &\text { Total cost in the year } 2025\\ &\begin{aligned} & =\text { RM40.58 }+ \text { RM7.50 } \\ & =\text { RM48.08 } \end{aligned} \end{aligned} $$
$$ \begin{aligned} &\text { RM48.08 > RM45 }\\ &\therefore \text { The allocated money is not enough. } \end{aligned} $$
Table 4 shows information for four ingredients used to produce a type of biscuit.

(a) Find the value of x, of y and of z.
[3 marks]
(b) The composite index for the production cost of the biscuit in the year 2023 with 2022 as the base year is 135.
(i) Find the ratio of ingredient A to ingredient B used.
(ii) The production cost of 200 biscuits in the year 2022 is RM25. The price of each ingredient is expected to increase by 20.25% from the year 2023 to the year 2025. In the year 2025, the box used to fit 40 biscuits is expected to cost RM1.50 per unit.
In the year 2025, if RM45 is allocated to produce 200 biscuits including the purchase of the box, determine whether or not the allocation is enough.
[7 marks]
Answer:
(a)
$$ \begin{aligned} \bar{I}_{\frac{23}{22}} & =130 \\ \frac{2.10}{x} \times 100 & =130 \\ \frac{2.10}{x} & =\frac{130}{100} \\ x & =\frac{2.10 \times 100}{130} \\ x & =1.62 \end{aligned} $$
$$ \begin{aligned} & y=\frac{2.40}{2.00} \times 100 \\ & y=120 \end{aligned} $$
$$ \begin{aligned} \bar{I}_{\frac{23}{22}} & =150 \\ \frac{z}{1.20} \times 100 & =150 \\ z & =\frac{150 \times 1.20}{100} \\ z & =1.80 \end{aligned} $$
(b)(i)
$$ \begin{aligned} \bar{I}_{\frac{23}{22}}=135 & \\ \frac{(130)(n)+(120)(m+n)+(160)\left(\frac{m}{3}\right)+(150)(2 n)}{n+m+n+\frac{m}{3}+2 n} & =135 \\ \frac{130 n+120 m+120 n+\frac{160}{3} m+300 n}{4 n+\frac{4}{3} m} & =135 \end{aligned} $$
$$ \begin{aligned} 550 n+\frac{520}{3} m & =135\left(4 n+\frac{4}{3} m\right) \\ 550 n+\frac{520}{3} m & =540 n+180 m \\ 550 n-540 n & =180 m-\frac{520}{3} m \\ 10 n & =\frac{20}{3} m \\ \frac{10}{\frac{20}{3}} & =\frac{m}{n} \\ \frac{3}{2} & =\frac{m}{n} \end{aligned} $$
$$ \therefore m: n=3: 2 $$
$$ \begin{aligned} & A: B=n: m+n \\ & A: B=2: 3+2 \\ & A: B=2: 5 \end{aligned} $$
(b)(ii)
$$ \begin{aligned} \bar{I}_{23 / 22} & =135 \\ \frac{P_{2023}}{P_{2022}} \times 100 & =135 \\ \frac{P_{2023}}{\mathrm{RM} 25} \times 100 & =135 \\ P_{2023} & =\frac{135 \times \mathrm{RM} 25}{100} \\ P_{2023} & =\mathrm{RM} 33.75 \end{aligned} $$
$$ \begin{aligned} \bar{I}_{25 / 23} & =100+20.25 \\ \frac{P_{2025}}{P_{2023}} \times 100 & =120.25 \\ \frac{P_{2025}}{\text { RM33.75 }} \times 100 & =120.25 \\ P_{2025} & =\frac{120.25 \times \text { RM33.75 }}{100} \\ P_{2025} & =\text { RM40.58 } \end{aligned} $$
$$ \begin{aligned} \text { Number of box } & =200 \div 40 \\ & =5 \end{aligned} $$
$$ \begin{aligned} \text { Price of box } & =5 \times \text { RM1.50 } \\ & =\text { RM7.50 } \end{aligned} $$
$$ \begin{aligned} &\text { Total cost in the year } 2025\\ &\begin{aligned} & =\text { RM40.58 }+ \text { RM7.50 } \\ & =\text { RM48.08 } \end{aligned} \end{aligned} $$
$$ \begin{aligned} &\text { RM48.08 > RM45 }\\ &\therefore \text { The allocated money is not enough. } \end{aligned} $$