Question 15:
(a) Diagram 12 shows a square and a rectangle.
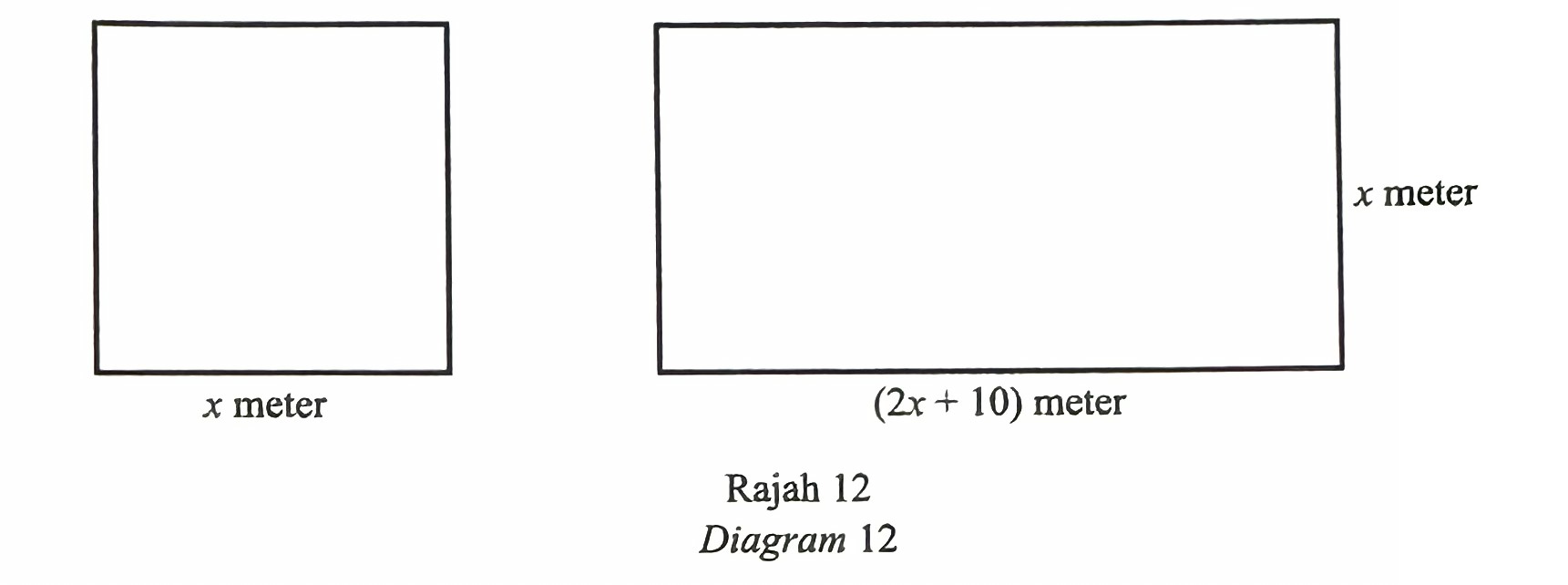Given that the sum of the areas of the shapes is more than 8 m2.
Using the table method, find the range of values of x.
[2 marks]
(b) A quadratic equation is given by x2 + 3x = -4p, such that p is a constant.
(i) Find the range of values of p if the equation has imaginary roots.
(ii) It is given that the equation has roots α and β. Form a quadratic equation with roots α – β + 1 and β – α + 1.
[6 marks]
Answer:
(a)
$$ \begin{aligned} (x)(x)+(2 x+10)(x) & >8 \\ x^2+2 x^2+10 x-8 & >0 \\ 3 x^2+10 x-8 & >0 \\ (3 x-2)(x+4) & >0 \end{aligned} $$
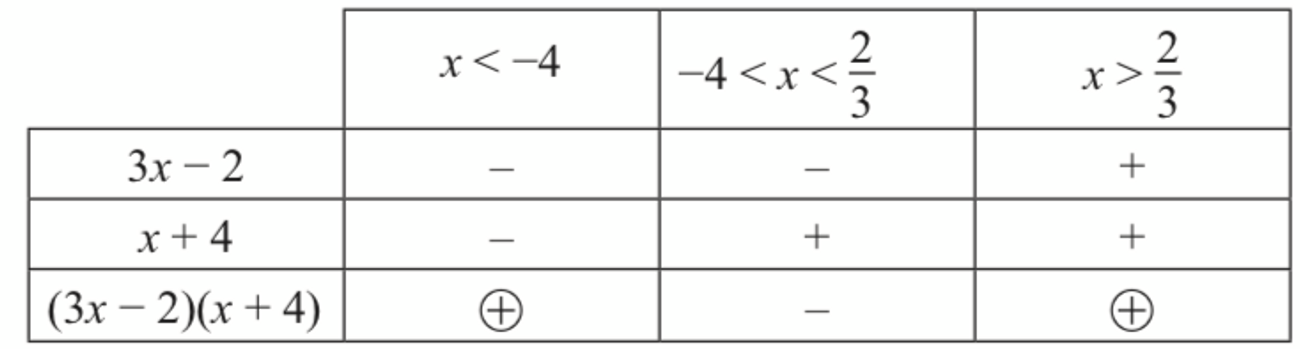$$
x>\frac{2}{3}, x<-4
$$
(b)(i)
$$ \begin{aligned} x^2+3 x & =-4 p \\ x^2+3 x+4 p & =0 \end{aligned} $$
$$ \begin{aligned} b^2-4 a c & <0 \\ (3)^2-4(1)(4 p) & <0 \\ 9-16 p & <0 \\ -16 p & <-9 \\ p & >\frac{9}{16} \end{aligned} $$
(b)(ii)
$$ \begin{aligned} & x^2+3 x+4 p=0 \\ & \text { Roots: } \alpha, \beta \\ & \text { SOR: } \alpha+\beta=-\frac{3}{1} \\ & \quad=-3 \end{aligned} $$
$$ \begin{aligned} \operatorname{POR} : \alpha \beta & =\frac{4 p}{1} \\ & =4 p \end{aligned} $$
$$ \text { New roots }=\alpha-\beta+1, \beta-\alpha+1 $$
$$ \begin{aligned} &\text { New SOR: }\\ &\begin{aligned} (\alpha-\beta+1)+(\beta-\alpha+1) & =\alpha-\beta+1+\beta-\alpha+1 \\ & =2 \end{aligned} \end{aligned} $$
$$ \begin{aligned} &\text { New POR: }\\ &\begin{aligned} (\alpha-\beta+1)(\beta-\alpha+1) & =\alpha \beta-\alpha^2+\alpha-\beta^2+\alpha \beta-\beta+\beta-\alpha+1 \\ & =-\alpha^2-\beta^2+2 \alpha \beta+1 \\ & =-\left(\alpha^2+\beta^2\right)+2 \alpha \beta+1 \\ & =-\left[(\alpha+\beta)^2-2 \alpha \beta\right]+2 \alpha \beta+1 \\ & =-(\alpha+\beta)^2+4 \alpha \beta+1 \\ & =-(-3)^2+4(4 p)+1 \\ & =-9+16 p+1 \\ & =-8+16 p \end{aligned} \end{aligned} $$
$$ \begin{array}{r} \text { New equation: } x^2-2 x+(-8+16 p)=0 \\ x^2-2 x+16 p-8=0 \end{array} $$
(a) Diagram 12 shows a square and a rectangle.
Given that the sum of the areas of the shapes is more than 8 m2.Using the table method, find the range of values of x.
[2 marks]
(b) A quadratic equation is given by x2 + 3x = -4p, such that p is a constant.
(i) Find the range of values of p if the equation has imaginary roots.
(ii) It is given that the equation has roots α and β. Form a quadratic equation with roots α – β + 1 and β – α + 1.
[6 marks]
Answer:
(a)
$$ \begin{aligned} (x)(x)+(2 x+10)(x) & >8 \\ x^2+2 x^2+10 x-8 & >0 \\ 3 x^2+10 x-8 & >0 \\ (3 x-2)(x+4) & >0 \end{aligned} $$
$$
x>\frac{2}{3}, x<-4
$$(b)(i)
$$ \begin{aligned} x^2+3 x & =-4 p \\ x^2+3 x+4 p & =0 \end{aligned} $$
$$ \begin{aligned} b^2-4 a c & <0 \\ (3)^2-4(1)(4 p) & <0 \\ 9-16 p & <0 \\ -16 p & <-9 \\ p & >\frac{9}{16} \end{aligned} $$
(b)(ii)
$$ \begin{aligned} & x^2+3 x+4 p=0 \\ & \text { Roots: } \alpha, \beta \\ & \text { SOR: } \alpha+\beta=-\frac{3}{1} \\ & \quad=-3 \end{aligned} $$
$$ \begin{aligned} \operatorname{POR} : \alpha \beta & =\frac{4 p}{1} \\ & =4 p \end{aligned} $$
$$ \text { New roots }=\alpha-\beta+1, \beta-\alpha+1 $$
$$ \begin{aligned} &\text { New SOR: }\\ &\begin{aligned} (\alpha-\beta+1)+(\beta-\alpha+1) & =\alpha-\beta+1+\beta-\alpha+1 \\ & =2 \end{aligned} \end{aligned} $$
$$ \begin{aligned} &\text { New POR: }\\ &\begin{aligned} (\alpha-\beta+1)(\beta-\alpha+1) & =\alpha \beta-\alpha^2+\alpha-\beta^2+\alpha \beta-\beta+\beta-\alpha+1 \\ & =-\alpha^2-\beta^2+2 \alpha \beta+1 \\ & =-\left(\alpha^2+\beta^2\right)+2 \alpha \beta+1 \\ & =-\left[(\alpha+\beta)^2-2 \alpha \beta\right]+2 \alpha \beta+1 \\ & =-(\alpha+\beta)^2+4 \alpha \beta+1 \\ & =-(-3)^2+4(4 p)+1 \\ & =-9+16 p+1 \\ & =-8+16 p \end{aligned} \end{aligned} $$
$$ \begin{array}{r} \text { New equation: } x^2-2 x+(-8+16 p)=0 \\ x^2-2 x+16 p-8=0 \end{array} $$