2.12.5 Quadratic Functions, SPM Practice (Paper 1 Question 21 – 25)

Question 21:
Given that the quadratic equation hx² – (h + 2)x – (h – 4) = 0 has real and distinc roots.  Find the range of values of h.

Solution:
$\begin{array}{l}\text{The quadratic equation }h{x}^2-\left(h+2\right)x-\left(h-4\right)=0\\ \text{has real and distinc roots}\text{.}\\ b^2-4ac>0\text{ is applied}\text{.}\\ {\left(-h-2\right)}^2-4\left(h\right)\left(-h+4\right)>0\\ h^2+4h+4+4h^2-16h>0\\ 5h^2-12h+4>0\\ \left(5h-2\right)\left(h-2\right)>0\\ \\ \text{The coefficient of }{h}^2\text{ is positive, }\\ \text{the region above the }x\text{-axis should be shaded}\text{.}\\ \left(5h-2\right)\left(h-2\right)=0\\ h=\frac{2}{5},2\end{array}$



$\begin{array}{l}\text{The range of values of }h\text{ for }\left(5h-2\right)\left(h-2\right)\text{>0 is}\\ h<\frac{2}{5}\text{ or }h>2.\end{array}$

Question 22:
The diagram below shows the graph of the quadratic function f(x) = (x + 3)² + 2h – 6, where h is a constant.


(a) State the equation of the axis of symmetry of the curve.
(b) Given the minimum value of the function is 4, find the value of h.

Solution:
(a)
When x + 3 = 0
 x = –3
Therefore, equation of the axis of symmetry of the curve is x = –3.

(b)
When x + 3 = 0, f(x) = 2h – 6
Minimum value of f(x) is 2h – 6.
2h – 6 = 4
2h = 10
h = 5

Question 23 (SPM 2017 – 4 marks):
The quadratic function f is defined by f(x) = x² + 4x + h, where h is a constant.
(a) Express f(x) in the form (x + m)² + n, where m and n are constants.

(b) Given the minimum value of f(x) is 8, find the value of h.

Solution:
(a)
f(x) = x² + 4x + h
  = x² + 4x + (2)² – (2)² + h
  = (x + 2)² – 4 + h

(b)
Given the minimum value of f(x) = 8
– 4 + h = 8
h = 12

Question 24 (SPM 2017 – 3 marks):
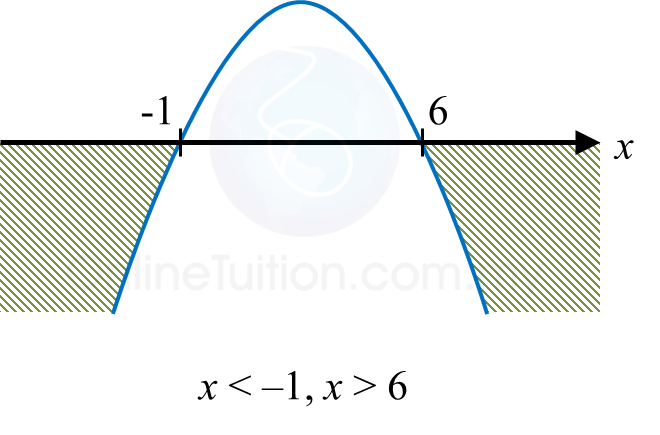
Find the range of values of x such that the quadratic function f(x) = 6 + 5x – x² is negative.

Solution:
(a)
f(x) < 0
6 + 5x – x² < 0
(6 – x)(x + 1) < 0
x < –1, x > 6

Question 25 (SPM 2017 – 4 marks):
(a) It is given that one of the roots of the quadratic equation x² + (p +3)x – p² = 0, where p is a constant, is negative of the other.
Find the value of the product of roots.

(b) It is given that the quadratic equation mx² – 5nx + 4m = 0, where m and n are constants, has two equal roots.
Find m : n.


Solution:
(a)
$\begin{array}{l}{x}^2+\left(p+3\right)x–p^2=0\\ a=1,b=p+3,c=-p^2\\ \text{Root 1}=\alpha ,\text{ Root 2}=-\alpha \\ \text{SOR}=-\frac{b}{a}\\ \alpha +\left(-\alpha \right)=-\frac{\left(p+3\right)}{1}\\ -\left(p+3\right)=0\\ p+3=0\\ p=-3\\ \\ POR=\frac{c}{a}\\ =\frac{-p^2}{1}\\ =-{\left(-3\right)}^2\\ =-9\end{array}$

(b)
$\begin{array}{l}m{x}^2-5nx+4m=0\\ a=m,b=-5n,c=4m\\ b^2=4ac\\ {\left(-5n\right)}^2=4\left(m\right)\left(4m\right)\\ 25n^2=16m^2\\ \frac{m^2}{n^2}=\frac{25}{16}\\ {\left(\frac{m}{n}\right)}^2={\left(\frac{5}{4}\right)}^2\\ \frac{m}{n}=\frac{5}{4}\\ m:n=5:4\end{array}$