Question 5:
The diameter of oranges harvested from a fruit orchard has a normal distribution with a mean of 3.2 cm and a variance of 2.25 cm.
Calculate
(a) the probability that an orange chosen at random from this fruit orchard has a diameter of more than 3.8 cm.
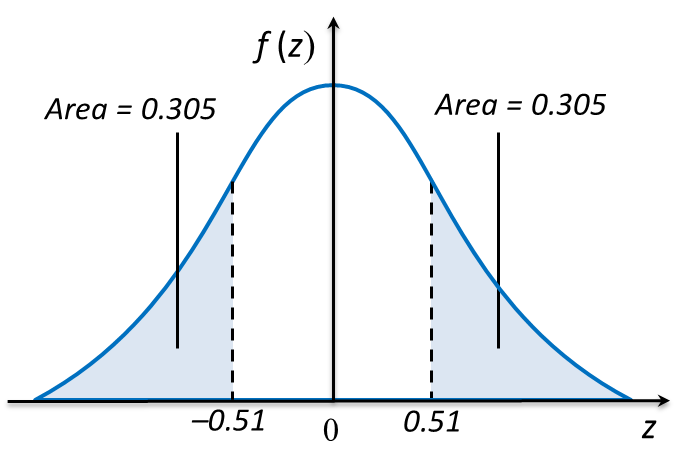
(b) the value of k if 30.5 % of the oranges have diameter less than k cm.
Solution:
µ = 3.2 cm
σ2 = 2.25cm
σ = √2.25 = 1.5 cm
Let X represents the diameter of an orange.
X ~ N (3.2, 1.52)
(a)
(b)
Question 6:
The masses of tomatoes in a farm are normally distributed with a mean of 130 g and standard deviation of 16 g. Tomato with weight more than 150 g is classified as grade ‘A’.
(a) A tomato is chosen at random from the farm. Find the probability that the tomato has a weight between 114 g and 150 g.
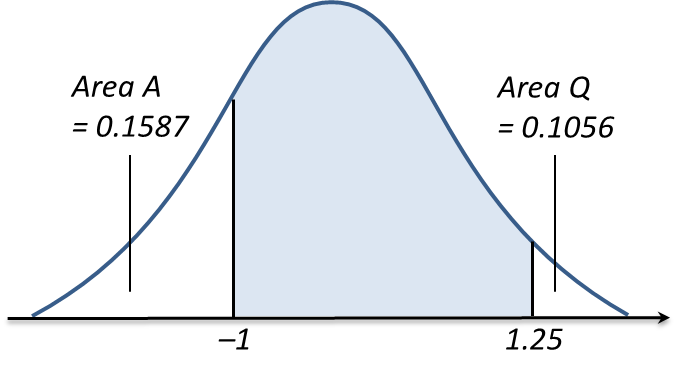
(b) It is found that 132 tomatoes in this farm are grade ‘A’. Find the total number of tomatoes in the farm.
Solution:
µ = 130
σ = 16
(a)
(b)
Probability of getting grade ‘A’ tomatoes,
P (X > 150) = P (Z > 1.25)
= 0.1056
Question 7:
In a boarding school entry exam, 300 students sat for a mathematics test. The marks obtained follow a normal distribution with a mean of 56 and a standard deviation of 8.
(a) Find the number of students who pass the test if the passing mark is 40.
(b) If 12% of the students pass the test with grade A, find the minimum mark to obtain grade A.
Solution:
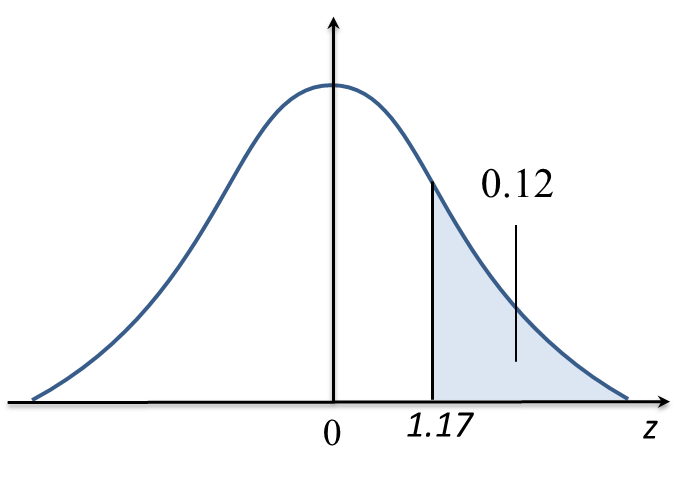 Thus, the minimum mark to obtain grade A is 66.
Thus, the minimum mark to obtain grade A is 66.
In a boarding school entry exam, 300 students sat for a mathematics test. The marks obtained follow a normal distribution with a mean of 56 and a standard deviation of 8.
(a) Find the number of students who pass the test if the passing mark is 40.
(b) If 12% of the students pass the test with grade A, find the minimum mark to obtain grade A.
Solution:
 Thus, the minimum mark to obtain grade A is 66.
Thus, the minimum mark to obtain grade A is 66.