Question 5:
The diameter of oranges harvested from a fruit orchard has a normal distribution with a mean of 3.2 cm and a variance of 2.25 cm.
Calculate
(a) the probability that an orange chosen at random from this fruit orchard has a diameter of more than 3.8 cm.
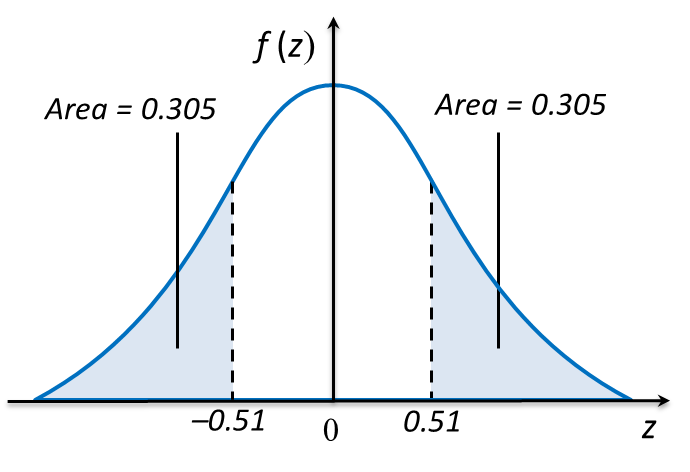
(b) the value of k if 30.5 % of the oranges have diameter less than k cm.
Solution:
µ = 3.2 cm
σ2 = 2.25cm
σ = √2.25 = 1.5 cm
Let X represents the diameter of an orange.
X ~ N (3.2, 1.52)
(a)
(b)
P(X<k)=0.305P(Z<k−3.21.5)=0.305From the standard normal distribution table,P(Z>0.51)=0.305P(Z<−0.51)=0.305k−3.21.5=−0.51k−3.2=−0.765k=2.435
Question 6:
The masses of tomatoes in a farm are normally distributed with a mean of 130 g and standard deviation of 16 g. Tomato with weight more than 150 g is classified as grade ‘A’.
(a) A tomato is chosen at random from the farm. Find the probability that the tomato has a weight between 114 g and 150 g.
(b) It is found that 132 tomatoes in this farm are grade ‘A’. Find the total number of tomatoes in the farm.
Solution:
µ = 130
σ = 16
(a)
P(114<X<150)=P(114−13016<Z<150−13016)=P(−1<Z<1.25)=1−P(Z>1)−P(Z>1.25)=1−0.1587−0.1056=0.7357
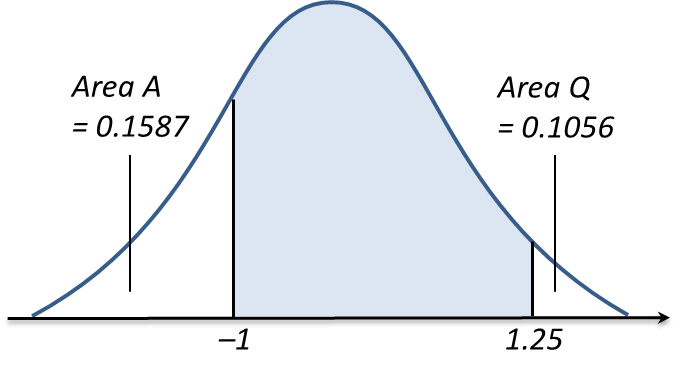
(b)
Probability of getting grade ‘A’ tomatoes,
P (X > 150) = P (Z > 1.25)
= 0.1056
Lets total number of tomatoes=N0.1056×N=132N=1320.1056N=1250
Question 7:
In a boarding school entry exam, 300 students sat for a mathematics test. The marks obtained follow a normal distribution with a mean of 56 and a standard deviation of 8.
(a) Find the number of students who pass the test if the passing mark is 40.
(b) If 12% of the students pass the test with grade A, find the minimum mark to obtain grade A.
Solution:
Let X=marks obtained by studentsX~N(56,82)(a) P(X≥40)=P(Z≥40−568) =P(Z≥−2) =1−P(Z≥2) =1−0.02275 =0.9773Number of students who pass the test=0.9773×300=293(b) Let the minimum mark to obtain grade A be kP(X≥k)=0.12P(Z≥k−568)=0.12 k−568=1.17 k=(1.17)(8)+56=65.36
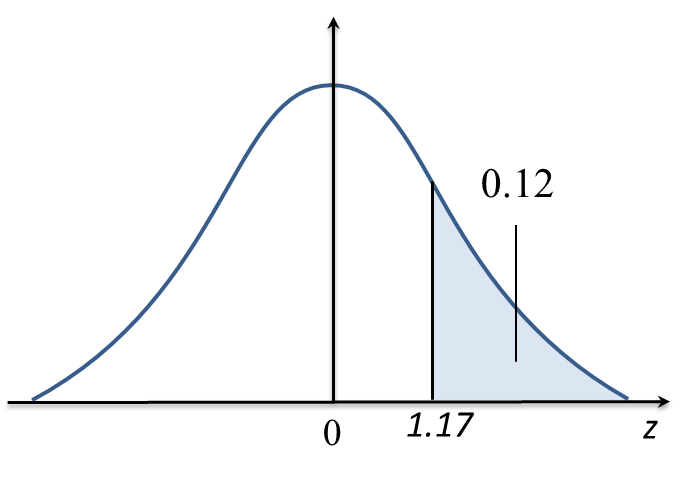Thus, the minimum mark to obtain grade A is 66.
In a boarding school entry exam, 300 students sat for a mathematics test. The marks obtained follow a normal distribution with a mean of 56 and a standard deviation of 8.
(a) Find the number of students who pass the test if the passing mark is 40.
(b) If 12% of the students pass the test with grade A, find the minimum mark to obtain grade A.
Solution:
Let X=marks obtained by studentsX~N(56,82)(a) P(X≥40)=P(Z≥40−568) =P(Z≥−2) =1−P(Z≥2) =1−0.02275 =0.9773Number of students who pass the test=0.9773×300=293(b) Let the minimum mark to obtain grade A be kP(X≥k)=0.12P(Z≥k−568)=0.12 k−568=1.17 k=(1.17)(8)+56=65.36
Thus, the minimum mark to obtain grade A is 66.