SPM Additional Mathematics 2018, Paper 1 (Question 5 – 7)

Question 5 (3 marks):
Find the value of
$\begin{array}{l}\left(\text{a}\right)\underset{x\to 1}{\lim }\left(7-x^2\right),\\ \left(\text{b}\right)f‘‘\left(2\right)\text{ if }f‘\left(x\right)=2x^3-4x+3.\end{array}$

Solution:
(a)
$\begin{array}{l}\underset{x\to 1}{\lim }\left(7-x^2\right)\\ =7-{\left(1\right)}^2\\ =6\end{array}$

(b)
$\begin{array}{l}f‘\left(x\right)=2x^3-4x+3\\ f‘‘\left(x\right)=6x^2-4\\ f‘‘\left(2\right)=6{\left(2\right)}^2-4\\ =24-4\\ =20\end{array}$

Question 6 (4 marks):
It is given that L = 4t – t² and x = 3 + 6t.
(a) Express $\frac{dL}{dx}$ in terms of t.
(b) Find the small change in x, when L changes from 3 to 3.4 at the instant t = 1.

Solution:
(a)
$\begin{array}{l}\text{Given }L=4t-t^2\text{ and }x=3+6t\\ L=4t-t^2\\ \frac{dL}{dt}=4-2t\\ \\ x=3+6t\\ \frac{dx}{dt}=6\\ \\ \frac{dL}{dx}=\frac{dL}{dt}\times \frac{dt}{dx}\\ \frac{dL}{dx}=\left(4-2t\right)\times \frac{1}{6}\\ =\frac{4-2t}{6}\\ =\frac{2-t}{3}\end{array}$


(b)
$\begin{array}{l}\delta L=3.4-3=0.4\\ \frac{\delta L}{\delta x}\approx \frac{dL}{dx}\\ \delta x=\delta L÷\frac{\delta L}{\delta x}\\ \delta x=\delta L\times \frac{\delta x}{\delta L}\\ =0.4\times \frac{3}{2-t}\\ =\frac{2}{5}\times \frac{3}{2-t}\\ =\frac{6}{5\left(2-t\right)}\\ \\ \text{When }t=1,\\ \delta x=\frac{6}{5\left(2-1\right)}=\frac{6}{5}\end{array}$

Question 7 (4 marks):
Diagram 2 shows the curve y = g(x). The straight line is a tangent to the curve.
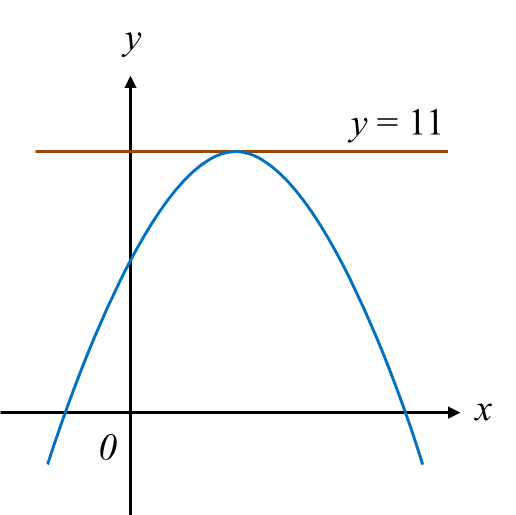Diagram 2

Given g’(x) = –4x + 8, find the equation of the curve.


Solution:
$\begin{array}{l}\text{Given }g‘\left(x\right)=-4x+8\\ \text{Maximum point when }g‘\left(x\right)=0\\ -4x+8=0\\ 4x=8\\ x=2\\ \text{Thus, maximum point is }\left(2,11\right).\\ \\ g‘\left(x\right)=-4x+8\\ {\displaystyle \int g‘\left(x\right)}={\displaystyle \int \left(-4x+8\right)}dx\\ g\left(x\right)=\frac{-4x^2}{2}+8x+c\\ g\left(x\right)=-2x^2+8x+c\\ \\ \text{Substitute }\left(2,11\right)\text{ into }g\left(x\right):\\ 11=-2{\left(2\right)}^2+8\left(2\right)+c\\ c=3\\ \\ \text{Thus, the equation of curve is}\\ g\left(x\right)=-2x^2+8x+3\end{array}$