Question 4 (7 marks):
Diagram 2 shows part of a rectangular wall painted with green, G, blue, B and purple, P subsequently.
The height of the wall is 2 m. The side length of the first coloured rectangle is 5 cm and the side length of each subsequent coloured rectangle increases by 3 cm.
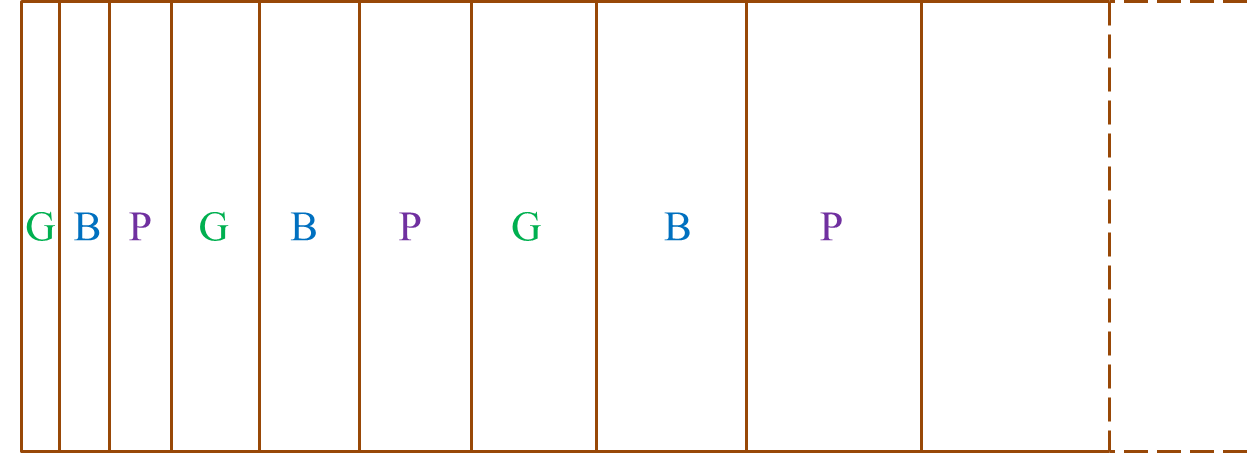
It is given that the total number of the coloured rectangles is 54.
(a) Find
(i) the side length, in cm, of the last coloured rectangle,
(ii) the total length, in cm, of the painted wall.
(b) Which coloured rectangle has an area of 28000 cm2?
Hence, state the colour of that particular rectangle.
Solution:
(a)
5, 8, 11, …
a = 5, d = 3
(i)
T54 = 1 + (54 – 1)d
= 5 + 53(3)
=164 cm
(ii)
(b)
Area of the first rectangle
= 2 m × 5 cm
= 200 × 5
= 1000 cm
Area of the second rectangle
= 200 × (5 + 3)
= 1600 cm
Area of the third rectangle
= 200 × (5 + 3 + 3)
= 2200 cm
1000, 1600, 2200, …
a = 1000, d = 600
Tn = 28 000
a + (n – 1)d = 28 000
1000 + (n – 1)600 = 28 000
600(n – 1) = 27 000
n – 1 = 45
n = 46
The colour of that particular rectangle is green.
Diagram 2 shows part of a rectangular wall painted with green, G, blue, B and purple, P subsequently.
The height of the wall is 2 m. The side length of the first coloured rectangle is 5 cm and the side length of each subsequent coloured rectangle increases by 3 cm.
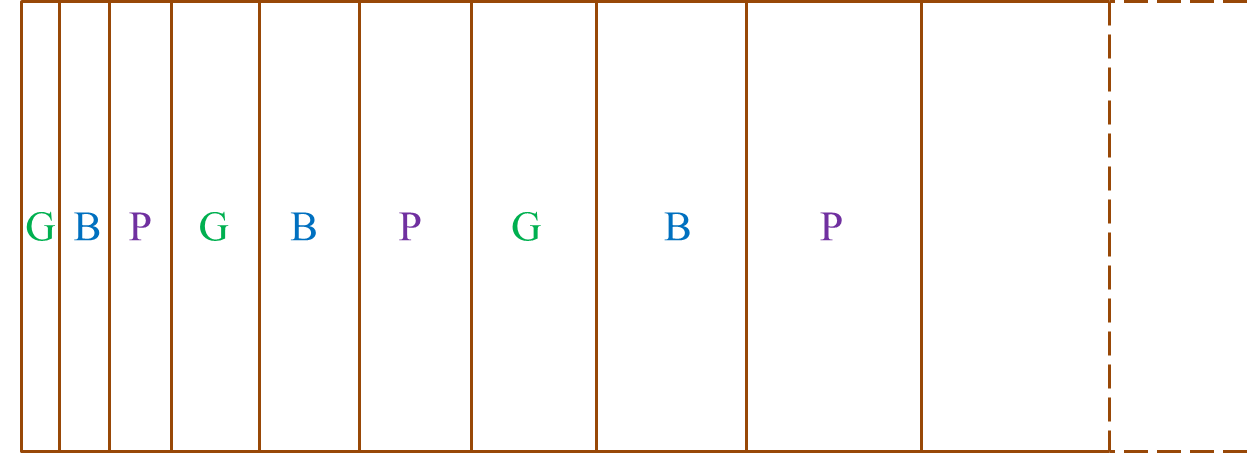
It is given that the total number of the coloured rectangles is 54.
(a) Find
(i) the side length, in cm, of the last coloured rectangle,
(ii) the total length, in cm, of the painted wall.
(b) Which coloured rectangle has an area of 28000 cm2?
Hence, state the colour of that particular rectangle.
Solution:
(a)
5, 8, 11, …
a = 5, d = 3
(i)
T54 = 1 + (54 – 1)d
= 5 + 53(3)
=164 cm
(ii)
(b)
Area of the first rectangle
= 2 m × 5 cm
= 200 × 5
= 1000 cm
Area of the second rectangle
= 200 × (5 + 3)
= 1600 cm
Area of the third rectangle
= 200 × (5 + 3 + 3)
= 2200 cm
1000, 1600, 2200, …
a = 1000, d = 600
Tn = 28 000
a + (n – 1)d = 28 000
1000 + (n – 1)600 = 28 000
600(n – 1) = 27 000
n – 1 = 45
n = 46
The colour of that particular rectangle is green.
Question 5 (7 marks):
Solution by scale drawing is not accepted.
Diagram 3 shows the locations of town M and town N drawn on a Cartesian plane.
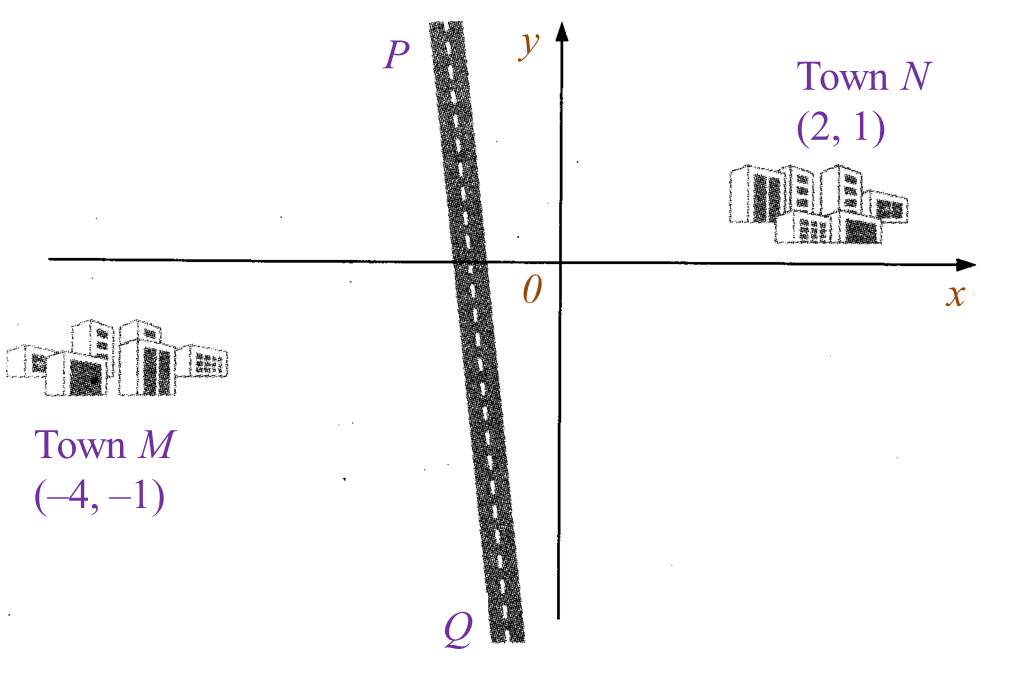
PQ is a straight road such that the distance from town M and town N to any point on the road is always equal.
(a) Find the equation of PQ.
(b) Another straight road, ST with an equation y = 2x + 7 is to be built.
(i) A traffic light is to be installed at the crossroads of the two roads.
Find the coordinates of the traffic light.
(ii) Which of the two roads passes through town L
Solution:
(a)
(b)(i)
(b)(ii)
Solution by scale drawing is not accepted.
Diagram 3 shows the locations of town M and town N drawn on a Cartesian plane.

PQ is a straight road such that the distance from town M and town N to any point on the road is always equal.
(a) Find the equation of PQ.
(b) Another straight road, ST with an equation y = 2x + 7 is to be built.
(i) A traffic light is to be installed at the crossroads of the two roads.
Find the coordinates of the traffic light.
(ii) Which of the two roads passes through town L
Solution:
(a)
(b)(i)
(b)(ii)