SPM Additional Mathematics 2017, Paper 2 (Question 1 – 3)

Question 1 (5 marks):
Solve the following simultaneous equations:
x – 3y = 1,
x² + 3xy + 9y² = 7


Solution:
$\begin{array}{l}x-3y=\mathrm{1\dots \dots \dots \dots \dots \dots .}\left(1\right)\\ x^2+3xy+9y^2=\mathrm{7\dots \dots \dots \dots \dots \dots .}\left(2\right)\\ \text{From }\left(1\right):x=3y+\mathrm{1\dots \dots \dots \dots \dots \dots .}\left(3\right)\\ \text{Substitute }\left(3\right)\text{ into }\left(2\right):\\ {\left(3y+1\right)}^2+3\left(3y+1\right)y+9y^2=7\\ 9y^2+6y+1+9y^2+3y+9y^2-7=0\\ 27y^2+9y-6=0\\ 9y^2+3y-2=0\\ \left(3y-1\right)\left(3y+2\right)=0\\ y=\frac{1}{3}\text{ or }-\frac{2}{3}\\ \\ \text{Substitute }y\text{ into }\left(3\right):\\ \text{When }y=\frac{1}{3}\\ x=3\left(\frac{1}{3}\right)+1=2\\ \text{When }y=-\frac{2}{3}\\ x=3\left(-\frac{2}{3}\right)+1=-1\\ \\ \text{Hence, the solutions are }x=2,y=\frac{1}{3}\text{ or }x=-1,y=-\frac{2}{3}.\end{array}$

Question 2 (7 marks):
It is given that the equation of a curve is $y=\frac{5}{x^2}.$  
(a) Find the value of $\frac{dy}{dx}$ when x = 3.
(b) Hence, estimate the value of $\frac{5}{{\left(2.98\right)}^2}.$  

Solution:
(a)
$\begin{array}{l}y=\frac{5}{x^2}=5x^{-2}\\ \frac{dy}{dx}=-10x^{-3}\\ =-\frac{10}{x^3}\\ \text{When }x=3\\ \frac{dy}{dx}=-\frac{10}{3^3}=-\frac{10}{27}\end{array}$


(b)
$\begin{array}{l}\delta x=2.98-3=-0.02\\ \delta y=\frac{dy}{dx}.\delta x\\ =-\frac{10}{27}\times \left(-0.02\right)\\ =0.007407\\ \\ \text{Values of }\frac{5}{{\left(2.98\right)}^2}\\ =y+\delta y\\ =\frac{5}{x^2}+\left(0.007407\right)\\ =\frac{5}{3^2}+\left(0.007407\right)\\ =0.56296\end{array}$

Question 3 (8 marks):
Diagram 1 shows a circle and a sector of a circle with a common centre O. The radius of the circle is r cm.

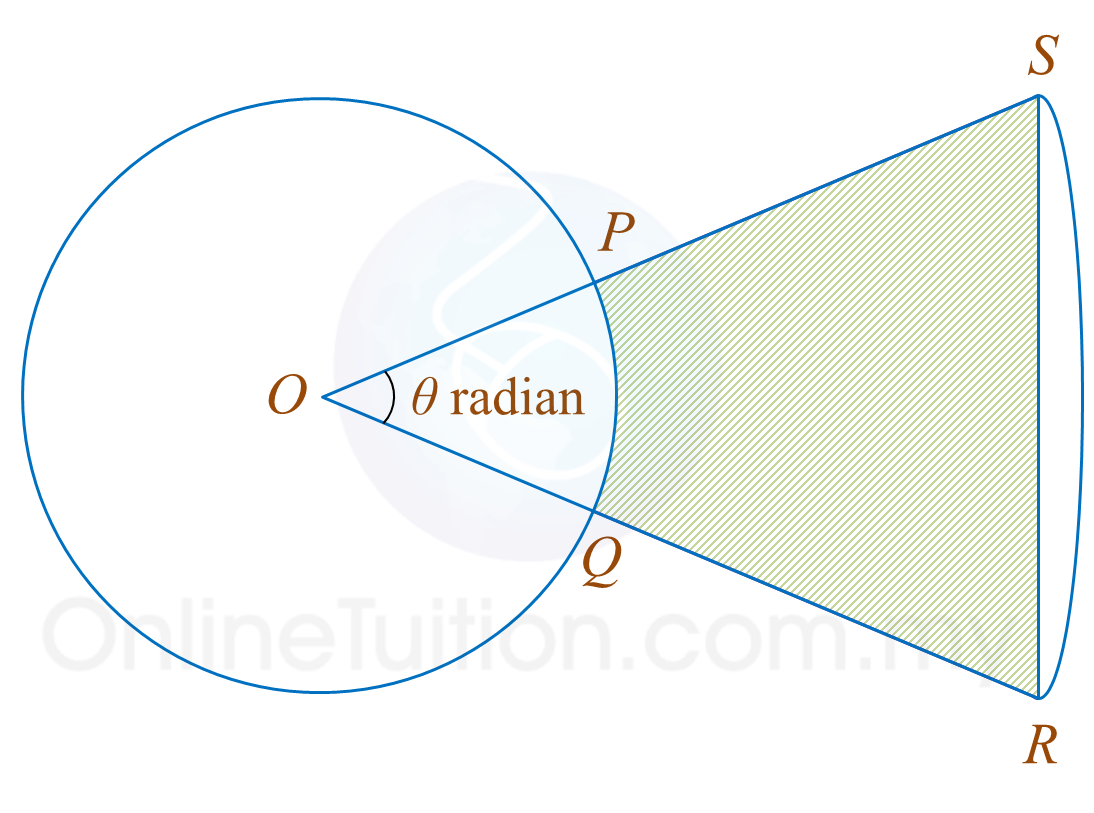
It is given that the length of arc PQ and arc RS are 2 cm and 7 cm respectively. QR = 10 cm.
[Use θ = 3.142]
Find
(a) the value of r and of θ,
(b) the area, in cm², of the shaded region.



Solution:
(a)
$\begin{array}{l}\text{Length of arc }PQ=2\text{ cm}\\ r\theta =2\mathrm{\dots \dots \dots \dots \dots ..}\left(1\right)\\ \\ \text{Length of arc }RS=7\text{ cm}\\ \left(r+10\right)\theta =7\\ r\theta +10\theta =7\mathrm{\dots \dots \dots \dots \dots ..}\left(2\right)\\ \\ \text{Substitute }\left(1\right)\text{ into }\left(2\right):\\ 2+10\theta =7\\ 10\theta =5\\ \theta =\frac{5}{10}\\ \theta =0.5\text{ rad}\\ \\ \text{From}\left(1\right):\\ \text{When }\theta =0.5\text{ rad,}\\ r\times 0.5=2\\ r=4\end{array}$

(b)
$\begin{array}{l}OS=OR=4+10=14\text{ cm}\\ \text{Area of shaded region}\\ =\text{area of }\Delta ORS-\text{ area of sector }OPQ\\ =\left(\frac{1}{2}\times {14}^2\times \sin 0.5\text{ rad}\right)-\left(\frac{1}{2}\times 4^2\times 0.5\right)\\ =42.981{\text{ cm}}^2\end{array}$