Question 6 (SPM 2018 – 6 marks):
Diagram 4 shows the front view of a part of a roller coaster track in a miniature park.
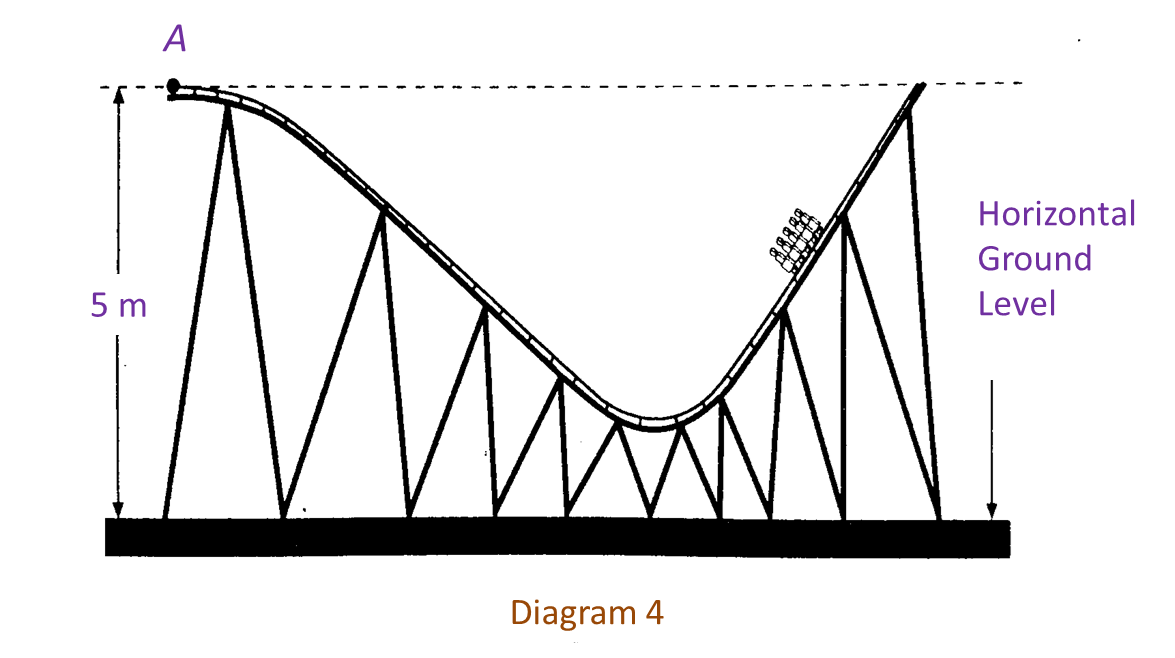
The curve part of the track of the roller coaster is represented by an equation , with point A as the region.
Find the shortest vertical distance, in m, from the track to ground level.
Solution:
Diagram 4 shows the front view of a part of a roller coaster track in a miniature park.

The curve part of the track of the roller coaster is represented by an equation , with point A as the region.
Find the shortest vertical distance, in m, from the track to ground level.
Solution:
Question 7 (SPM 2019):
Diagram 1 shows a sector POA with centre O.
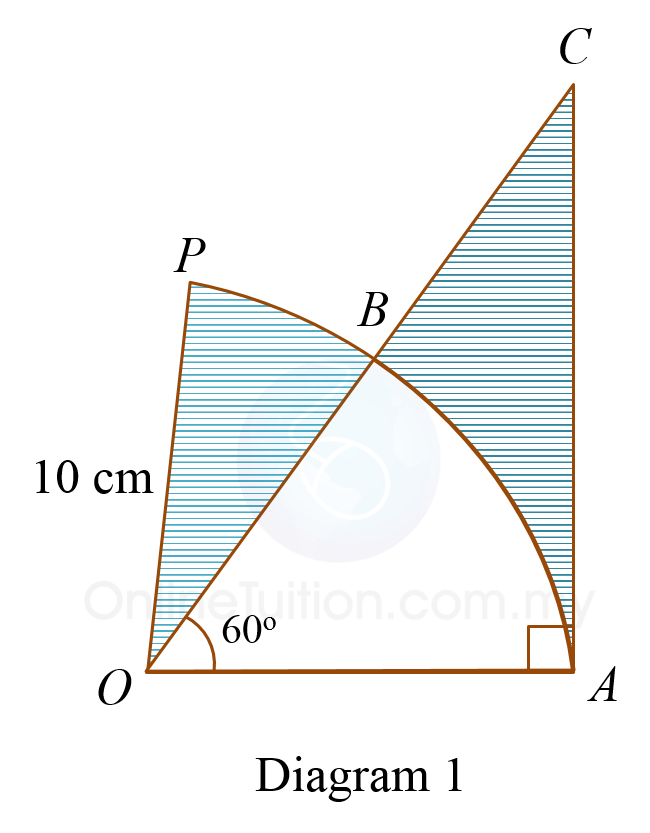
It is given that the length of arc PB is 2.56 cm. [Use π = 3.142]
Calculate
(a) ∠ POB in radians, [2 marks]
(b) the area, in cm2, of the shaded region. [4 marks]
Solution:
(a)
(b)
Diagram 1 shows a sector POA with centre O.

It is given that the length of arc PB is 2.56 cm. [Use π = 3.142]
Calculate
(a) ∠ POB in radians, [2 marks]
(b) the area, in cm2, of the shaded region. [4 marks]
Solution:
(a)
(b)