Question 7:
Without drawing graph or using method of differentiation, find the maximum or minimum value of the function y = 2 + 4x – 3x2. Hence, find the equation of the axis of symmetry of the graph.
Solution:
By completing the square for the function in the form of y = a(x + p)2+ q to find the maximum or minimum value of the function.
y = 2 + 4x – 3x2
y = – 3x2 + 4x + 2 ← (in general form)
Since a = –3 < 0,
Therefore, the function y has a maximum value of
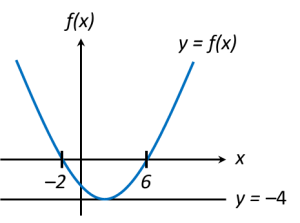
The diagram above shows the graph of a quadratic function y = f(x). The straight line y = –4 is tangent to the curve y = f(x).
(a) Write the equation of the axis of symmetry of the function f(x).
(b) Express f(x) in the form of (x + p)2 + q , where p and q are constant.
(c) Find the range of values of x so that
(i) f(x) < 0, (ii) f(x) ≥ 0.
Solution:
(a)
x-coordinate of the minimum point is the midpoint of (–2, 0) and (6, 0)
=
Therefore, equation of the axis of symmetry of the function f(x) is x = 2.
(b)
Substitute x = 2 into x + p = 0,
2 + p = 0
p = –2
and q = –4 (the smallest value of f(x))
Therefore, f(x) = (x + p)2 + q
f(x) = (x – 2)2 – 4
(c)(i) From the graph, for f(x) < 0, range of values of x are –2 < x < 6 ← (below x-axis).
(c)(ii) From the graph, for f(x) ≥ 0, range of values of x are x ≤ –2 or x ≥ 6 ← (above x-axis).
Question 9:
Given that the quadratic function f(x) = 2x2 – px + p has a minimum value of –18 at x = 1.
(a) Find the values of p and q.
(b) With the value of p and q found in (a), find the values of x, where graph f(x) cuts the x-axis.
(c) Hence, sketch the graph of f(x).
Solution:
(a)
(b)
(c)
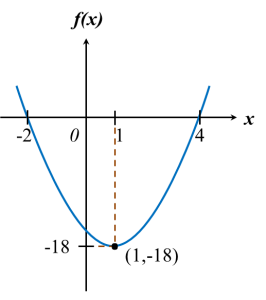
Given that the quadratic function f(x) = 2x2 – px + p has a minimum value of –18 at x = 1.
(a) Find the values of p and q.
(b) With the value of p and q found in (a), find the values of x, where graph f(x) cuts the x-axis.
(c) Hence, sketch the graph of f(x).
Solution:
(a)
(b)
(c)

Question 10:
(a) Find the range of values of k if the equation x2 – kx + 3k – 5 = 0 does not have real roots.
(b) Show that the quadratic equation hx2 – (h + 3)x + 1 = 0 has real and distinc roots for all values of h.
Solution:
(a)
Graph function y = (k – 2)(k – 10) cuts the horizontal line at k = 2 and k = 10 when b2 – 4ac < 0.

The range of values of k that satisfy the inequality above is 2 < k < 10.
(b)
The minimum value of (h + 1) + 8 is 8, a positive value. Therefore, b2 – 4ac > 0 for all values of h.
Hence, quadratic equation hx2 – (h + 3)x + 1 = 0 has real and distinc roots for all values of h.
(a) Find the range of values of k if the equation x2 – kx + 3k – 5 = 0 does not have real roots.
(b) Show that the quadratic equation hx2 – (h + 3)x + 1 = 0 has real and distinc roots for all values of h.
Solution:
(a)
Graph function y = (k – 2)(k – 10) cuts the horizontal line at k = 2 and k = 10 when b2 – 4ac < 0.

The range of values of k that satisfy the inequality above is 2 < k < 10.
(b)
The minimum value of (h + 1) + 8 is 8, a positive value. Therefore, b2 – 4ac > 0 for all values of h.
Hence, quadratic equation hx2 – (h + 3)x + 1 = 0 has real and distinc roots for all values of h.