Question 11 (SPM 2018 – 7 marks):
Mathematics Society of SMK Mulia organized a competition to design a logo for the society.

Diagram 3 shows the circular logo designed by Adrian. The three blue coloured regions are congruent. It is given that the perimeter of the blue coloured region is 20π cm.
[Use π = 3.142]
Find
(a) the radius, in cm, of the logo to the nearest integer,
(b) the area, in cm2, of the yellow coloured region.
Solution:
(a)
(b)

Mathematics Society of SMK Mulia organized a competition to design a logo for the society.

Diagram 3 shows the circular logo designed by Adrian. The three blue coloured regions are congruent. It is given that the perimeter of the blue coloured region is 20π cm.
[Use π = 3.142]
Find
(a) the radius, in cm, of the logo to the nearest integer,
(b) the area, in cm2, of the yellow coloured region.
Solution:
(a)
(b)

Question 12 (SPM 2019):
Diagram 1 shows a sector POA with centre O.
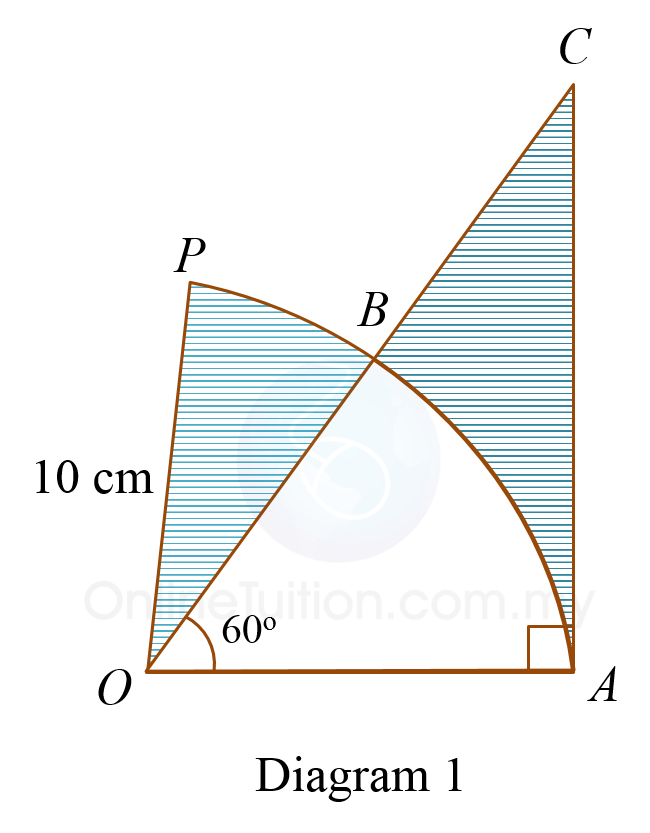
It is given that the length of arc PB is 2.56 cm. [Use π = 3.142]
Calculate
(a) ∠ POB in radians, [2 marks]
(b) the area, in cm2, of the shaded region. [4 marks]
Solution:
(a)
(b)
Diagram 1 shows a sector POA with centre O.

It is given that the length of arc PB is 2.56 cm. [Use π = 3.142]
Calculate
(a) ∠ POB in radians, [2 marks]
(b) the area, in cm2, of the shaded region. [4 marks]
Solution:
(a)
(b)
Question 13 (SPM 2005):
Diagram 6 shows a sector POQ of a circle, centre O. The point A lies on OP, the point B lies on OQ and AB is perpendicular to OQ.
$$ \text { The length of } O A=8 \mathrm{~cm} \text { and } \angle P O Q=\frac{\pi}{6} \text { radian. } $$
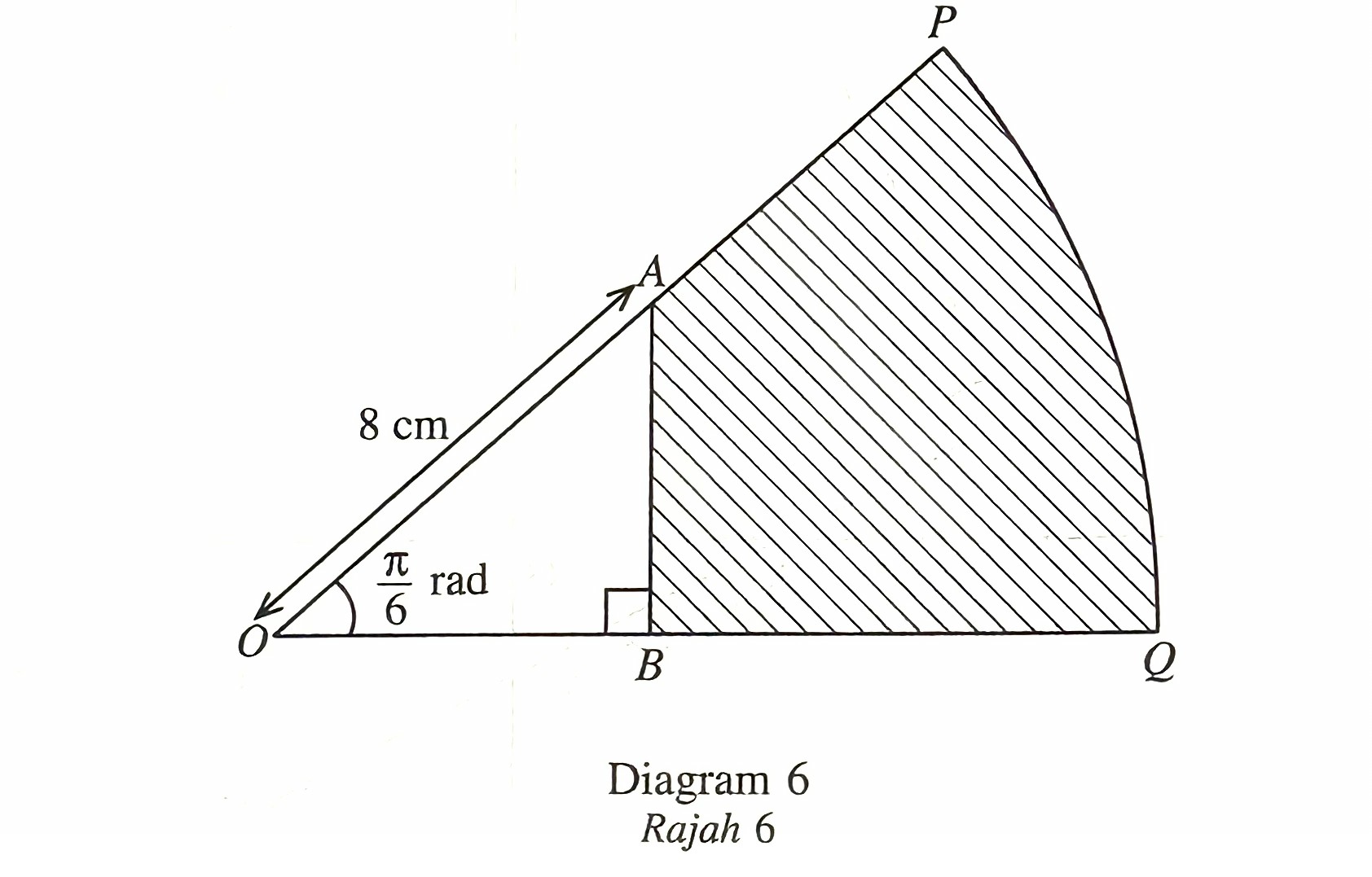
It is given that OA : OP = 4 : 7.
[Use π = 3.142]
Calculate
(a) the length, in cm, of AP. [1 mark]
(b) the perimeter, in cm , of the shaded region. [5 marks]
(c) the area, in cm2, of the shaded region. [4 marks]
Answer:
(a)
$$ A P=\frac{3}{4} \times 8 \mathrm{~cm}=6 \mathrm{~cm} $$
(b)
$$ \begin{aligned} & A B=8 \sin \frac{\pi}{6}=4 \mathrm{~cm} \\ & O Q=O P=14 \mathrm{~cm} \\ & B Q=14-8 \cos \frac{\pi}{6} \end{aligned} $$
$$ \begin{aligned} &\text { Perimeter of the shaded region }\\ &\begin{aligned} & =A P+A B+B Q+\operatorname{Arc} P Q \\ & =6+4+\left(14-8 \cos \frac{\pi}{6}\right)+14\left(\frac{\pi}{6}\right) \\ & =6+4+7.072+7.331 \\ & =24.40 \mathrm{~cm} \end{aligned} \end{aligned} $$
(c)
$$ \begin{aligned} & \text { Area of the shaded region } \\ & =\text { Area of sector } P O Q-\text { Area of } \triangle O A B \\ & =\frac{1}{2}\left(14^2\right)\left(\frac{\pi}{6}\right)-\frac{1}{2}(4)\left(8 \cos \frac{\pi}{6}\right) \\ & =37.46 \mathrm{~cm}^2 \end{aligned} $$
Diagram 6 shows a sector POQ of a circle, centre O. The point A lies on OP, the point B lies on OQ and AB is perpendicular to OQ.
$$ \text { The length of } O A=8 \mathrm{~cm} \text { and } \angle P O Q=\frac{\pi}{6} \text { radian. } $$

It is given that OA : OP = 4 : 7.
[Use π = 3.142]
Calculate
(a) the length, in cm, of AP. [1 mark]
(b) the perimeter, in cm , of the shaded region. [5 marks]
(c) the area, in cm2, of the shaded region. [4 marks]
Answer:
(a)
$$ A P=\frac{3}{4} \times 8 \mathrm{~cm}=6 \mathrm{~cm} $$
(b)
$$ \begin{aligned} & A B=8 \sin \frac{\pi}{6}=4 \mathrm{~cm} \\ & O Q=O P=14 \mathrm{~cm} \\ & B Q=14-8 \cos \frac{\pi}{6} \end{aligned} $$
$$ \begin{aligned} &\text { Perimeter of the shaded region }\\ &\begin{aligned} & =A P+A B+B Q+\operatorname{Arc} P Q \\ & =6+4+\left(14-8 \cos \frac{\pi}{6}\right)+14\left(\frac{\pi}{6}\right) \\ & =6+4+7.072+7.331 \\ & =24.40 \mathrm{~cm} \end{aligned} \end{aligned} $$
(c)
$$ \begin{aligned} & \text { Area of the shaded region } \\ & =\text { Area of sector } P O Q-\text { Area of } \triangle O A B \\ & =\frac{1}{2}\left(14^2\right)\left(\frac{\pi}{6}\right)-\frac{1}{2}(4)\left(8 \cos \frac{\pi}{6}\right) \\ & =37.46 \mathrm{~cm}^2 \end{aligned} $$
Question 14 (SPM 2006):
Diagram 4 shows the plan of a garden.
PCQ is a semicircle with centre O and has a radius of 8 m.
RAQ is a sector of a circle with centre A and has a radius of 14 m.
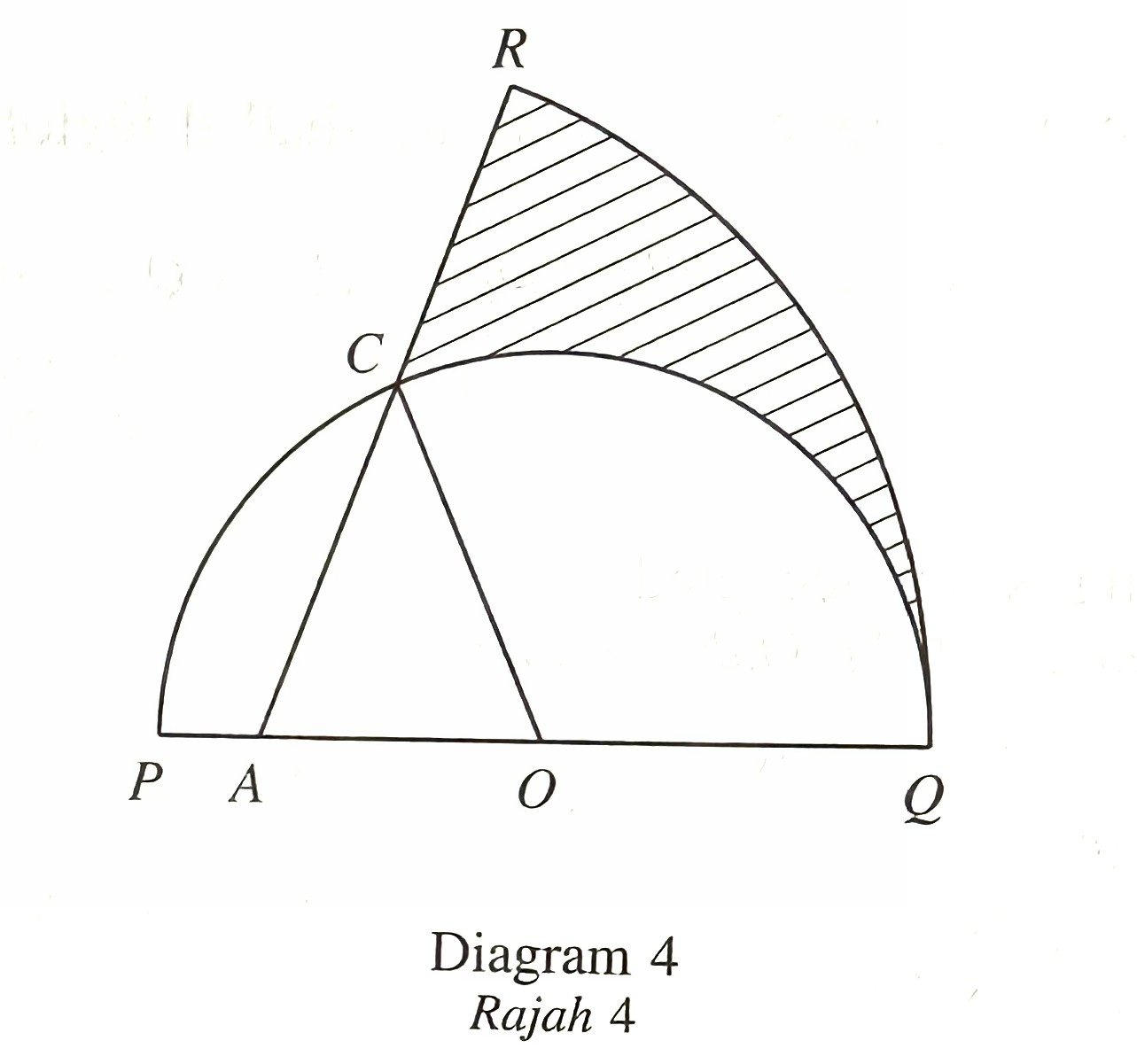
Sector COQ is a lawn. The shaded region is a flower bed and has to be fenced. It is given that AC = 8 m and ∠COQ = 1.956 radians.
[Use π = 3.142]
Calculate
(a) the area, in m2, of the lawn. [2 marks]
(b) the length, in m, of the fence required for fencing the flower bed. [4 marks]
(c) the area, in m2, of the flower bed. [4 marks]
Answer:
(a)
$$ \begin{aligned} & \text { Area of the lawn } \\ & =\text { Area of sector } C O Q \\ & =\frac{1}{2}\left(8^2\right)(1.956) \\ & =62.59 \mathrm{~m}^2 \end{aligned} $$
(b)
$$ \begin{aligned} & A C=O C=8 \mathrm{~m} \\ & \begin{aligned} \angle C A O & =\angle C O A \\ & =3.142-1.956 \\ & =1.186 \text { radians } \end{aligned} \end{aligned} $$
$$ \begin{aligned} &R C=14-8=6 \mathrm{~m}\\ &\text { Length of the fence required }\\ &\begin{aligned} & =R C+\operatorname{Arc} C Q+\operatorname{Arc} R Q \\ & =6+8(1.956)+14(1.186) \\ & =38.25 \mathrm{~m} \end{aligned} \end{aligned} $$
(c)
Area of the flower bed
= Area of sector RAQ – Area of sector COQ – Area Δ CAO
$$ \begin{aligned} = & \frac{1}{2}\left(14^2\right)(1.186)-\frac{1}{2}\left(8^2\right)(1.956) \\ & -\frac{1}{2}(8)(6) \sin 1.186 \\ = & 31.39 \mathrm{~m}^2 \end{aligned} $$
Diagram 4 shows the plan of a garden.
PCQ is a semicircle with centre O and has a radius of 8 m.
RAQ is a sector of a circle with centre A and has a radius of 14 m.

Sector COQ is a lawn. The shaded region is a flower bed and has to be fenced. It is given that AC = 8 m and ∠COQ = 1.956 radians.
[Use π = 3.142]
Calculate
(a) the area, in m2, of the lawn. [2 marks]
(b) the length, in m, of the fence required for fencing the flower bed. [4 marks]
(c) the area, in m2, of the flower bed. [4 marks]
Answer:
(a)
$$ \begin{aligned} & \text { Area of the lawn } \\ & =\text { Area of sector } C O Q \\ & =\frac{1}{2}\left(8^2\right)(1.956) \\ & =62.59 \mathrm{~m}^2 \end{aligned} $$
(b)
$$ \begin{aligned} & A C=O C=8 \mathrm{~m} \\ & \begin{aligned} \angle C A O & =\angle C O A \\ & =3.142-1.956 \\ & =1.186 \text { radians } \end{aligned} \end{aligned} $$
$$ \begin{aligned} &R C=14-8=6 \mathrm{~m}\\ &\text { Length of the fence required }\\ &\begin{aligned} & =R C+\operatorname{Arc} C Q+\operatorname{Arc} R Q \\ & =6+8(1.956)+14(1.186) \\ & =38.25 \mathrm{~m} \end{aligned} \end{aligned} $$
(c)
Area of the flower bed
= Area of sector RAQ – Area of sector COQ – Area Δ CAO
$$ \begin{aligned} = & \frac{1}{2}\left(14^2\right)(1.186)-\frac{1}{2}\left(8^2\right)(1.956) \\ & -\frac{1}{2}(8)(6) \sin 1.186 \\ = & 31.39 \mathrm{~m}^2 \end{aligned} $$
Question 15 (SPM 2009):
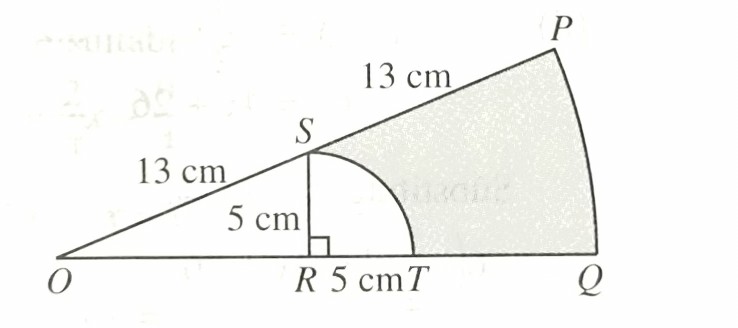
In Diagram 10, POQ is a sector of a circle with centre O and radius 26 cm. SRT is a quadra of a circle with centre R and radius 5 cm.
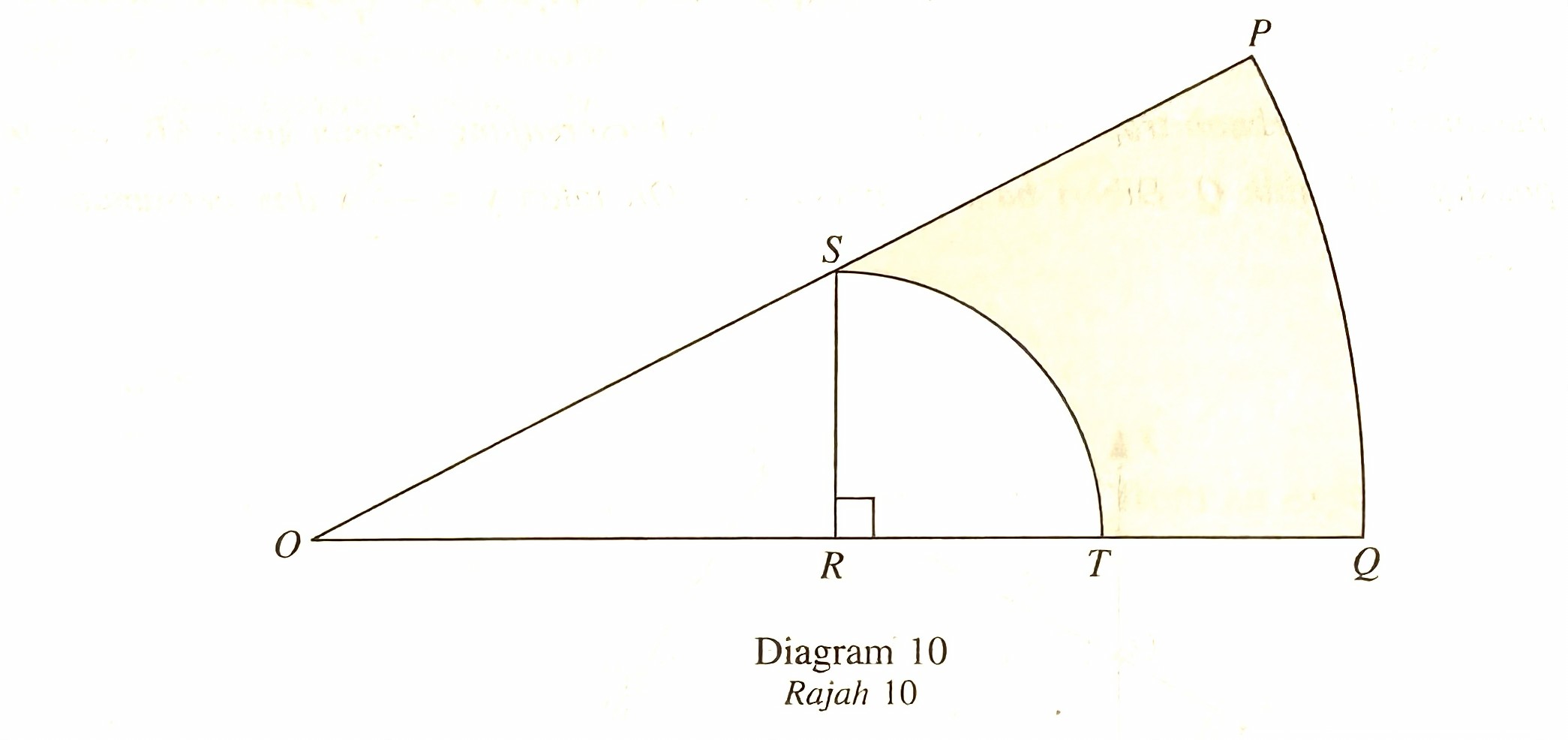
It is given that S is the midpoint of OP.
Use π = 3.142 and give the answers correct to two decimal places.
Calculate
(a) ∠POQ, in radian. [2 marks]
(b) the perimeter, in cm, of the coloured region. [4 marks]
(c) the area, in cm2, of the coloured region. [4 marks]
Answer:
(a)
$$ \text { In } \begin{aligned} \triangle S O R, \sin \angle P O Q & =\frac{5}{13} \\ \angle P O Q & =0.39 \text { radian } \end{aligned} $$
(b)
$$ \begin{aligned} &\begin{aligned} & O R=\sqrt{13^2-5^2}=12 \mathrm{~cm} \\ & T Q=26-12-5=9 \mathrm{~cm} \end{aligned}\\ &\text { Perimeter of the coloured region }\\ &\begin{aligned} & =13+9+\frac{1}{4} \times 2 \pi(5)+26(0.39) \\ & =40.00 \mathrm{~cm} \end{aligned} \end{aligned} $$
(c)
$$ \begin{aligned} &\text { Area of the coloured region }\\ &\begin{aligned} = & \text { Area of sector } P O Q-\text { Area of quadrant } S R T \\ & – \text { Area of } \triangle S O R \\ = & \frac{1}{2}\left(26^2\right)(0.39)-\frac{1}{4} \times \pi\left(5^2\right)-\frac{1}{2}(12)(5) \\ = & 82.18 \mathrm{~cm}^2 \end{aligned} \end{aligned} $$
In Diagram 10, POQ is a sector of a circle with centre O and radius 26 cm. SRT is a quadra of a circle with centre R and radius 5 cm.

It is given that S is the midpoint of OP.
Use π = 3.142 and give the answers correct to two decimal places.
Calculate
(a) ∠POQ, in radian. [2 marks]
(b) the perimeter, in cm, of the coloured region. [4 marks]
(c) the area, in cm2, of the coloured region. [4 marks]
Answer:

(a)
$$ \text { In } \begin{aligned} \triangle S O R, \sin \angle P O Q & =\frac{5}{13} \\ \angle P O Q & =0.39 \text { radian } \end{aligned} $$
(b)
$$ \begin{aligned} &\begin{aligned} & O R=\sqrt{13^2-5^2}=12 \mathrm{~cm} \\ & T Q=26-12-5=9 \mathrm{~cm} \end{aligned}\\ &\text { Perimeter of the coloured region }\\ &\begin{aligned} & =13+9+\frac{1}{4} \times 2 \pi(5)+26(0.39) \\ & =40.00 \mathrm{~cm} \end{aligned} \end{aligned} $$
(c)
$$ \begin{aligned} &\text { Area of the coloured region }\\ &\begin{aligned} = & \text { Area of sector } P O Q-\text { Area of quadrant } S R T \\ & – \text { Area of } \triangle S O R \\ = & \frac{1}{2}\left(26^2\right)(0.39)-\frac{1}{4} \times \pi\left(5^2\right)-\frac{1}{2}(12)(5) \\ = & 82.18 \mathrm{~cm}^2 \end{aligned} \end{aligned} $$