Question 10:
Diagram 4 shows the curve y = px3, such that p is a constant. The tangent to the curve at point A intersects the y-axis at B(0, -4).
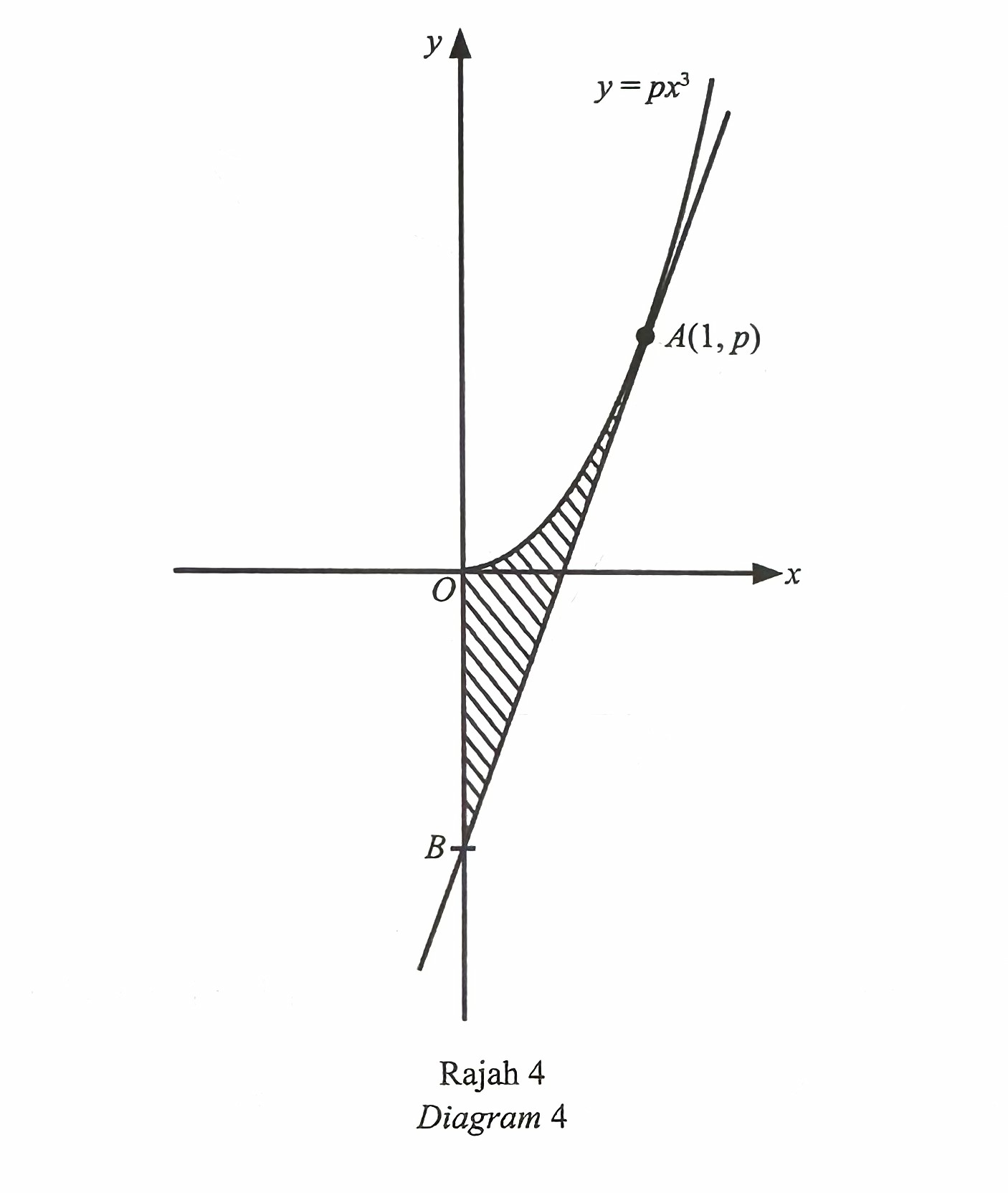Calculate
(a) the value of p, [4 marks]
(b) the area of the shaded region, [4 marks]
(c) the volume generated, in terms of π, when the region bounded by the curve and the straight line x = 1 is revolved through 90o about the x-axis. [2 marks]
Answer:
(a)
$$ \begin{aligned} & y=p x^3 \\ & \frac{\mathrm{~d} y}{\mathrm{~d} x}=3 p x^2 \end{aligned} $$
$$ \begin{aligned} \frac{\mathrm{d} y}{\mathrm{~d} x} \text { passes } A(1, p)=m_{A B} & : \\ 3 p(1)^2 & =\frac{-4-p}{0-1} \\ 3 p & =\frac{-4-p}{-1} \\ -3 p & =-4-p \\ -3 p+p & =-4 \\ -2 p & =-4 \\ p & =\frac{-4}{-2} \\ p & =2 \end{aligned} $$
(b)
Equation tangent passes A(1, 2) : $$ \begin{aligned} y-2 & =\frac{-4-2}{0-1}(x-1) \\ y-2 & =6(x-1) \\ y & =6 x-6+2 \\ y & =6 x-4 \end{aligned} $$ When y = 0, $$ \begin{aligned} 6 x-4 & =0 \\ 6 x & =4 \\ x & =\frac{2}{3} \end{aligned} $$
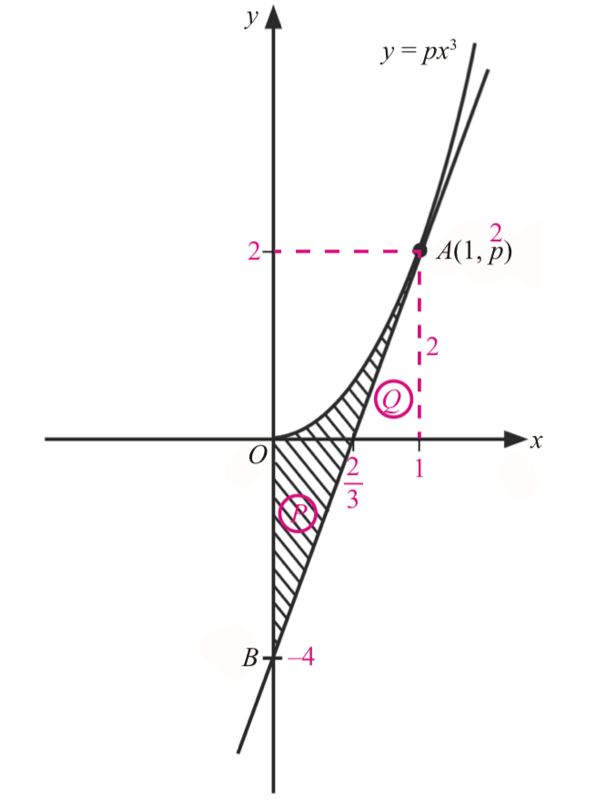
Area, $$ \begin{aligned} \Delta P & =\frac{1}{2} \times \frac{2}{3} \times 4 \\ & =\frac{4}{3} \end{aligned} $$ Area, $$ \begin{aligned} \Delta Q & =\frac{1}{2} \times\left(1-\frac{2}{3}\right) \times 2 \\ & =\frac{1}{3} \end{aligned} $$
$$ \begin{aligned} \text { Shaded area } & =\int_0^1 2 x^3 \mathrm{~d} x-\frac{1}{3}+\frac{4}{3} \\ & =\left[\frac{2 x^4}{4}\right]_0^1-\frac{1}{3}+\frac{4}{3} \\ & =\left[\left(\frac{2(1)^4}{4}\right)\right]-\left(\frac{2(0)^4}{4}\right)+1 \\ & =\left(\frac{1}{2}-0\right)+1 \\ & =\frac{1}{2}+1 \\ & =\frac{3}{2} \end{aligned} $$
(c)
$$ \begin{aligned} \text { Volume } & =\frac{1}{4} \pi \int_0^1\left(2 x^3\right)^2 \mathrm{~d} x \\ & =\frac{1}{4} \pi \int_0^1 4 x^6 \mathrm{~d} x \\ & =\frac{1}{4} \pi\left[\frac{4 x^7}{7}\right]_0^1 \\ & =\frac{1}{4} \pi\left[\frac{4(1)^7}{7}\right]-\left[\frac{4(0)^7}{7}\right] \\ & =\frac{1}{4}\left(\frac{4}{7}\right) \pi \text { unit }^3 \\ & =\frac{1}{7} \pi \text { unit }^3 \end{aligned} $$
Diagram 4 shows the curve y = px3, such that p is a constant. The tangent to the curve at point A intersects the y-axis at B(0, -4).
Calculate(a) the value of p, [4 marks]
(b) the area of the shaded region, [4 marks]
(c) the volume generated, in terms of π, when the region bounded by the curve and the straight line x = 1 is revolved through 90o about the x-axis. [2 marks]
Answer:
(a)
$$ \begin{aligned} & y=p x^3 \\ & \frac{\mathrm{~d} y}{\mathrm{~d} x}=3 p x^2 \end{aligned} $$
$$ \begin{aligned} \frac{\mathrm{d} y}{\mathrm{~d} x} \text { passes } A(1, p)=m_{A B} & : \\ 3 p(1)^2 & =\frac{-4-p}{0-1} \\ 3 p & =\frac{-4-p}{-1} \\ -3 p & =-4-p \\ -3 p+p & =-4 \\ -2 p & =-4 \\ p & =\frac{-4}{-2} \\ p & =2 \end{aligned} $$
(b)
Equation tangent passes A(1, 2) : $$ \begin{aligned} y-2 & =\frac{-4-2}{0-1}(x-1) \\ y-2 & =6(x-1) \\ y & =6 x-6+2 \\ y & =6 x-4 \end{aligned} $$ When y = 0, $$ \begin{aligned} 6 x-4 & =0 \\ 6 x & =4 \\ x & =\frac{2}{3} \end{aligned} $$
Area, $$ \begin{aligned} \Delta P & =\frac{1}{2} \times \frac{2}{3} \times 4 \\ & =\frac{4}{3} \end{aligned} $$ Area, $$ \begin{aligned} \Delta Q & =\frac{1}{2} \times\left(1-\frac{2}{3}\right) \times 2 \\ & =\frac{1}{3} \end{aligned} $$
$$ \begin{aligned} \text { Shaded area } & =\int_0^1 2 x^3 \mathrm{~d} x-\frac{1}{3}+\frac{4}{3} \\ & =\left[\frac{2 x^4}{4}\right]_0^1-\frac{1}{3}+\frac{4}{3} \\ & =\left[\left(\frac{2(1)^4}{4}\right)\right]-\left(\frac{2(0)^4}{4}\right)+1 \\ & =\left(\frac{1}{2}-0\right)+1 \\ & =\frac{1}{2}+1 \\ & =\frac{3}{2} \end{aligned} $$
(c)
$$ \begin{aligned} \text { Volume } & =\frac{1}{4} \pi \int_0^1\left(2 x^3\right)^2 \mathrm{~d} x \\ & =\frac{1}{4} \pi \int_0^1 4 x^6 \mathrm{~d} x \\ & =\frac{1}{4} \pi\left[\frac{4 x^7}{7}\right]_0^1 \\ & =\frac{1}{4} \pi\left[\frac{4(1)^7}{7}\right]-\left[\frac{4(0)^7}{7}\right] \\ & =\frac{1}{4}\left(\frac{4}{7}\right) \pi \text { unit }^3 \\ & =\frac{1}{7} \pi \text { unit }^3 \end{aligned} $$