Question 1:
Given g(x)=2x−53x−p, x≠q
(a)(i) Express p in terms of q and find g-1 (x) in term of p.
(a)(ii) Given gn−1(x)=px−53x−2, x≠k ,
determine the value of n by comparing the g-1 (x) above with the given gn-1 (x).
Next, find the value of k. [5 marks]
(b) What is the condition on p so that g = g-1 ? [1 mark]
Solution:
(a)(i)
3x−p≠03x≠px≠p3as x≠q∴q=p3p=3qg(x)=2x−53x−pLet g−1(x)=yg(y)=x2y−53y−p=x2y−5=3xy−pxy(2−3x)=−px+5y(3x−2)=px−5y=px−53x−2∴g−1(x)=px−53x−2
(a)(ii)
gn−1(x)=g−1(x)=px−53x−2∴n−1=−1n=03x−2≠0x≠23k=23
(b)
g(x)=2x−53x−pg−1(x)=px−53x−2g(x)=g−1(x) if p=2
Given g(x)=2x−53x−p, x≠q
(a)(i) Express p in terms of q and find g-1 (x) in term of p.
(a)(ii) Given gn−1(x)=px−53x−2, x≠k ,
determine the value of n by comparing the g-1 (x) above with the given gn-1 (x).
Next, find the value of k. [5 marks]
(b) What is the condition on p so that g = g-1 ? [1 mark]
Solution:
(a)(i)
3x−p≠03x≠px≠p3as x≠q∴q=p3p=3qg(x)=2x−53x−pLet g−1(x)=yg(y)=x2y−53y−p=x2y−5=3xy−pxy(2−3x)=−px+5y(3x−2)=px−5y=px−53x−2∴g−1(x)=px−53x−2
(a)(ii)
gn−1(x)=g−1(x)=px−53x−2∴n−1=−1n=03x−2≠0x≠23k=23
(b)
g(x)=2x−53x−pg−1(x)=px−53x−2g(x)=g−1(x) if p=2
Question 2:
Find the range of values of x for 5 < 2x2 + x + 4 and 2x2 + x + 4 ≤ 10.
Hence, solve the inequality 5 < 2x2+ x + 4 ≤ 10.
[4 marks]
Solution:
5 < 2x2 + x + 4
0 < 2x2 + x – 1
2x2 + x – 1 > 0
(2x – 1)(x + 1) > 0
x < -1 or x > ½
2x2 + x + 4 ≤ 10
2x2 + x – 6 ≤ 0
(2x – 3)(x + 2) ≤ 0
-2 ≤ x ≤ 3/2
x < -1, x > ½ or -2 ≤ x ≤ 3/2
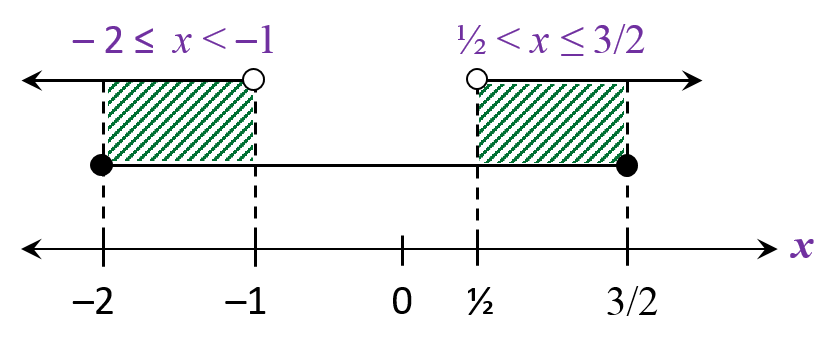-2 ≤ x < -1 or ½ < x ≤ 3/2
Find the range of values of x for 5 < 2x2 + x + 4 and 2x2 + x + 4 ≤ 10.
Hence, solve the inequality 5 < 2x2+ x + 4 ≤ 10.
[4 marks]
Solution:
5 < 2x2 + x + 4
0 < 2x2 + x – 1
2x2 + x – 1 > 0
(2x – 1)(x + 1) > 0
x < -1 or x > ½
2x2 + x + 4 ≤ 10
2x2 + x – 6 ≤ 0
(2x – 3)(x + 2) ≤ 0
-2 ≤ x ≤ 3/2
x < -1, x > ½ or -2 ≤ x ≤ 3/2
-2 ≤ x < -1 or ½ < x ≤ 3/2