SPM Additional Mathematics 2018, Paper 1 (Question 23 – 25)

Question 23 (4 marks):
Diagram 10 shows the position of three campsites A, B and C at a part of a riverbank drawn on a Cartesian plane, such that A and B lie on the same straight riverbank.

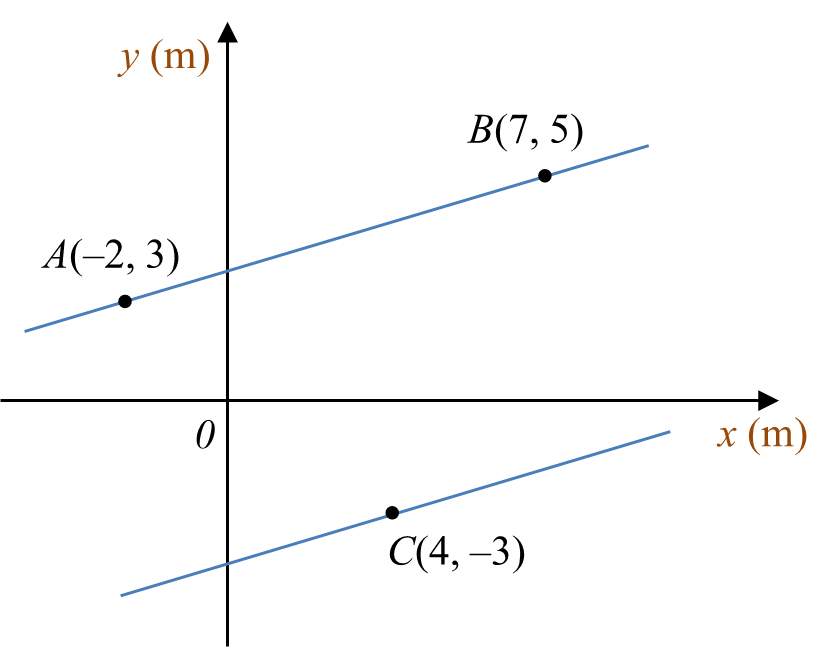Diagram 10

Sam wants to cross the river from campsite C to the opposite riverbank where the campsites A and B are located.
Find the shortest distance, in m, that he can take to cross the river. Give your answer correct to four decimal places.


Solution:

$\begin{array}{l}\text{Let the shortest distance from campsite }C\\ \text{to opposite riverbank is }CD\text{.}\\ \text{Area of }△ABC\\ =\frac{1}{2}|\begin{array}{l}-2\text{ 7 4 }\\ \text{ 3 }5-\text{3 }\end{array}\begin{array}{l}-2\\ \text{ 3}\end{array}|\\ =\frac{1}{2}|\left(-2\right)\left(5\right)+\left(7\right)\left(-3\right)+\left(4\right)\left(3\right)\\ -\left(3\right)\left(7\right)-\left(5\right)\left(4\right)-\left(-3\right)\left(-2\right)|\\ =\frac{1}{2}|-66|\\ =33{\text{ units}}^2\\ \\ \text{Distance of }AB\\ =\sqrt{{\left(-2-7\right)}^2+{\left(3-5\right)}^2}\\ =\sqrt{85}\text{ m}\\ \\ \text{Area of }△ABC=33\\ \frac{1}{2}\left(AB\right)\left(CD\right)=33\\ \frac{1}{2}\left(\sqrt{85}\right)\left(CD\right)=33\\ CD=\frac{33\left(2\right)}{\sqrt{85}}\\ CD=7.1587\left(4\text{ d}\text{.p}\text{.}\right)\\ \\ \text{Thus, the shortest distance is 7}\text{.1587 m}\text{.}\end{array}$

Question 24 (4 marks):
A voluntary body organizes a first aid course 4 times per month, every Saturday from March until September.
[Assume there are four Saturdays in every month]

Salmah intends to join the course but she might need to spare a Saturday per month to accompany her mother to the hospital. The probability that Salmah will attend the course each Saturday is 0.8. Salmah will be given a certificate of monthly attendance if she can attend the course at least 3 times a month.

(a) Find the probability that Salmah will be given the certificate of monthly attendance.

(b) Salmah will qualify to sit for the first aid test if she obtains more than 5 certificates of monthly attendance.
Find the probability that Salmah qualifies to take the first aid test.


Solution:
(a)

$\begin{array}{l}P\left(X=r\right)={}^{n}C{}_r{p}^r{q}^{n-r}\\ p=0.8,q=0.2,n=4,r=3,4\\ \\ P\left(X\ge 3\right)\\ =P\left(X=3\right)+P\left(X=4\right)\\ ={}^{4}C{}_3{\left(0.8\right)}^3{\left(0.2\right)}^1+{}^{4}C{}_4{\left(0.8\right)}^4{\left(0.2\right)}^0\\ =0.4096+0.4096\\ =0.8192\end{array}$

(b)

$\begin{array}{l}P\left(X=r\right)={}^{n}C{}_r{p}^r{q}^{n-r}\\ p=0.8192,q=0.1808,n=7,r=6,\text{ 7}\\ \\ P\left(X>5\right)\\ =P\left(X=6\right)+P\left(X=7\right)\\ ={}^{7}C{}_6{\left(0.8192\right)}^6{\left(0.1808\right)}^1+\\ {}^{7}C{}_7{\left(0.8192\right)}^7{\left(0.1808\right)}^0\\ =0.3825+0.2476\\ =0.6301\end{array}$