6.3.3 Sketching Graphs of Trigonometric Functions (Part 2)

6.3.3 Sketching Graphs of Trigonometric Functions (Part 2)

Example 2:

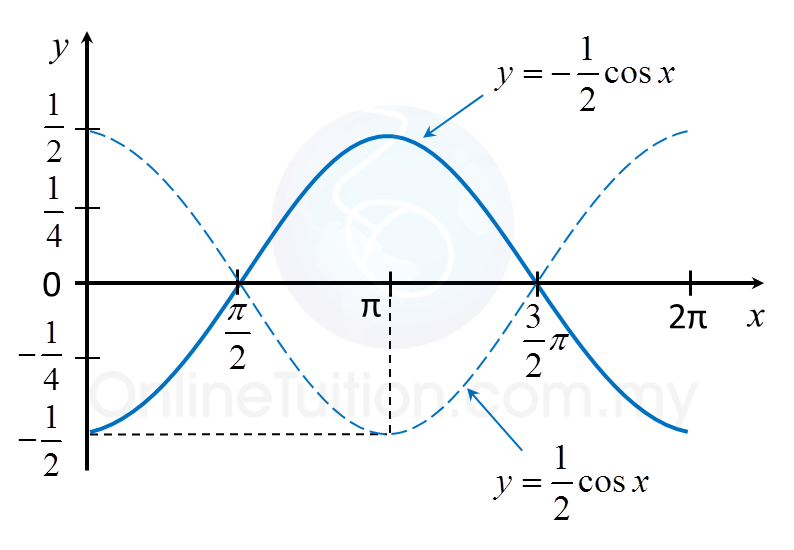
(a) Sketch the graph y = –½ cos x for 0 ≤ x ≤ 2π.

(b) Hence, using the same axes, sketch a suitable graph to find the number of solutions to the equation

\frac{π}{2 x} + \cos x = 0

for 0 ≤ x ≤ 2π.

State the number of solutions.

Solution:

(a)

(b)

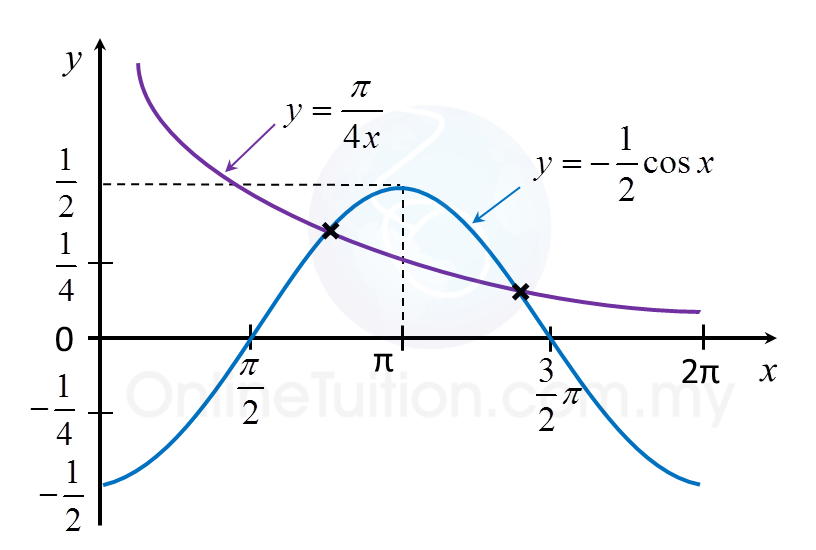
\begin{array}{l} \frac{π}{2 x} + \cos x = 0 \\ \frac{π}{2 x} = - \cos x \\ \frac{π}{4 x} = - \frac{1}{2} \cos x \leftarrow Multiply both sides by \frac{1}{2} \\ y = \frac{π}{4 x} \leftarrow y = - \frac{1}{2} \cos x \end{array}

The suitable graph to draw is

y = \frac{π}{4 x} .

x	$\frac{π}{2}$	π	2π
$y = \frac{π}{4 x}$	½	¼	⅛

From the graphs, there are two points of intersection for 0 ≤ x ≤ 2π.

Number of solutions = 2.