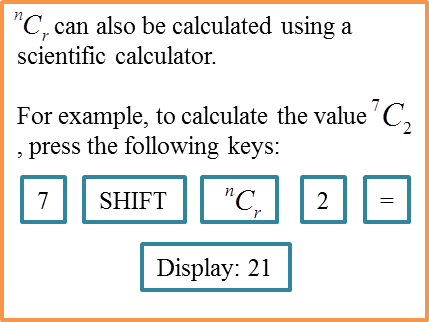
4.3 Combinations - SPM Additional Mathematics

4.3 Combinations

(1) The number of combinations of r objects chosen from n different objects is given by :

^{n} C_{r} = \frac{n!}{r! (n - r)!}

(2) A combination of r objects chosen from n different objects is a selection of a set of r objects chosen from n objects. The order of the objects in the chosen set is not taken into consideration.

\begin{array}{l} N o t e : \\ (i)^{n} C_{0} = 1 \\ (i i)^{n} C_{n} = 1 \\ (i i i)^{n} C_{r} =^{n} C_{n - r} \end{array}

Example 1:

\begin{array}{l} {Calculate the value of}^{7} C_{2} \\ ^{7} C_{2} = \frac{7!}{(7 - 2)! \times 2!} \\ = \frac{7!}{5! \times 2!} \\ = \frac{7 \times 6 \times 5!}{5! \times 2!} \\ = \frac{7 \times 6}{2 \times 1} \\ = 21 \end{array}

Calculator Computation:

Example 2:

There are 6 marbles, each with different colour, which are to be divided equally between 2 children. Find the number of different ways the division of the marbles can be done.

Solution:

Number of ways giving 3 marbles to the first child =

^{6} C_{3}

Number of ways giving the remaining 3 marbles =

^{3} C_{3}

So, the number of different ways the division of the marbles

\begin{array}{l} =^{6} C_{3} \times^{3} C_{3} \\ = 20 \times 1 \\ = 20 \end{array}

Leave a Comment Cancel reply