3.5 Integration as the Summation of Areas
(A) Area of the region between a Curve and the x-axis.
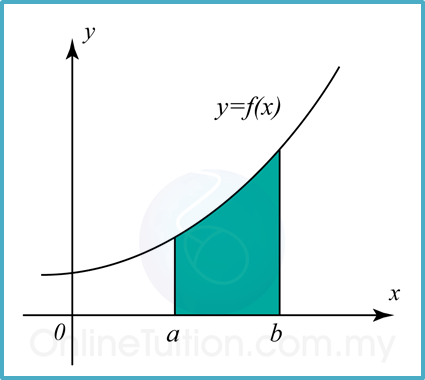
(A) Area of the region between a Curve and the x-axis.
Area of the shaded region;
A=∫baydx
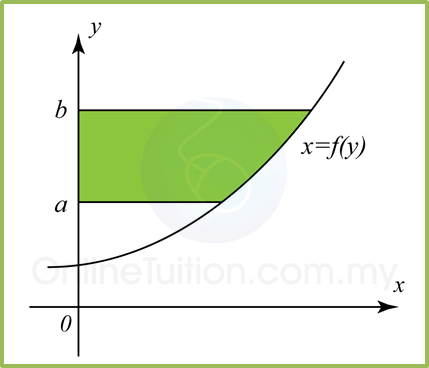
(B) Area of the region between a curve and the y-axis.
Area of the shaded region;
A=∫baxdy
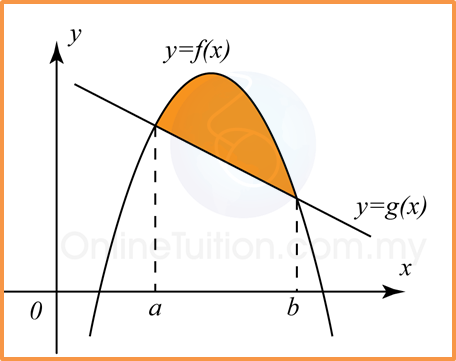
(C) Area of the region between a curve and a straight line.
Area of the shaded region;
A=∫baf(x)dx−∫bag(x)dx
Example 1
Find the area of the shaded region.
Solution:
Area of the shaded region=∫baydx=∫40(6x−x2)dx=[6x22−x33]40=[3(4)2−(4)33]−0=2623unit2
Example 2
Find the area of the shaded region.
Solution:
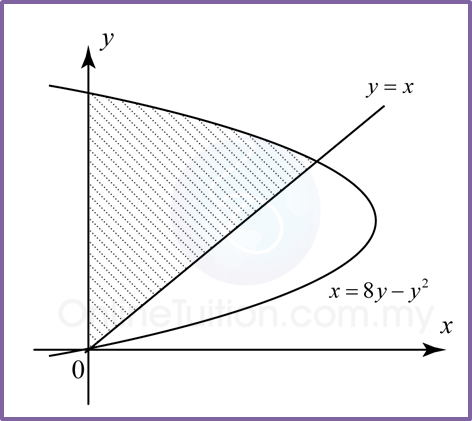
Find the area of the shaded region.
Solution:
Area of the shaded region=∫baydx=∫40(6x−x2)dx=[6x22−x33]40=[3(4)2−(4)33]−0=2623unit2
Example 2
Find the area of the shaded region.
Solution:
y = x —–(1)
x = 8y – y2—–(2)
Substitute (1) into (2),
y = 8y – y2
y2 – 7y = 0
y (y – 7) = 0
y = 0 or 7
From (1), x = 0 or 7
Therefore the intersection points of the curve and the straight line is (0, 0) and (7, 7).
Intersection point of the curve and y-axis is,
x = 8y – y2
At y-axis, x = 0
0 = 8y – y2
y (y – 8) = 0
y = 0, 8
Area of shaded region = (A1) Area of triangle + (A2) Area under the curve from y = 7 to y = 8.
=12×base×height +∫87xdy=12×(7)(7)+∫87(8y−y2)dy=492+[8y22−y33]87=2412+[4(8)2−(8)33]−[4(7)2−(7)33]=2412+8513−8123=2816unit2