Question 4
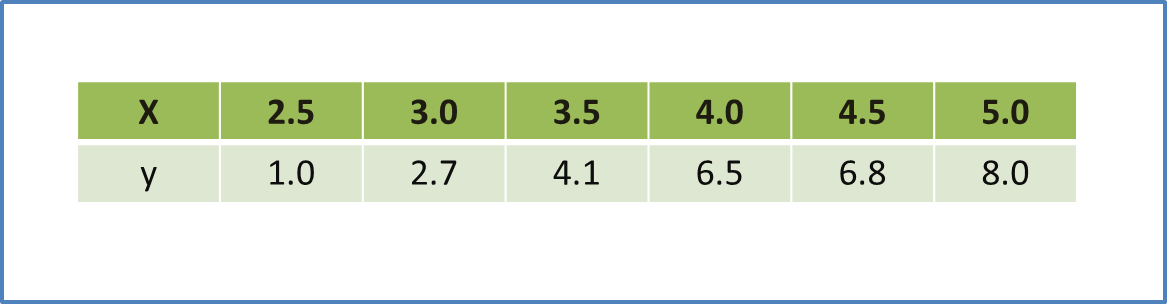
The table below shows the corresponding values of two variables, x and y, that are related by the equation , where p and q are constants.
One of the values of y is incorrectly recorded.
(a) Using scale of 2 cm to 5 units on the both axis, plot the graph of xy against . Hence, draw the line of best fit
(b) Use your graph in (a) to answer the following questions:
(i) State the values of y which is incorrectly recorded and determine its actual value.
(ii) Find the value of p and of q.
The table below shows the corresponding values of two variables, x and y, that are related by the equation , where p and q are constants.
One of the values of y is incorrectly recorded.
(a) Using scale of 2 cm to 5 units on the both axis, plot the graph of xy against . Hence, draw the line of best fit
(b) Use your graph in (a) to answer the following questions:
(i) State the values of y which is incorrectly recorded and determine its actual value.
(ii) Find the value of p and of q.
Solution
Step 1 : Construct a table consisting X and Y.
Step 2 : Plot a graph of Y against X, using the scale given and draw a line of best fit
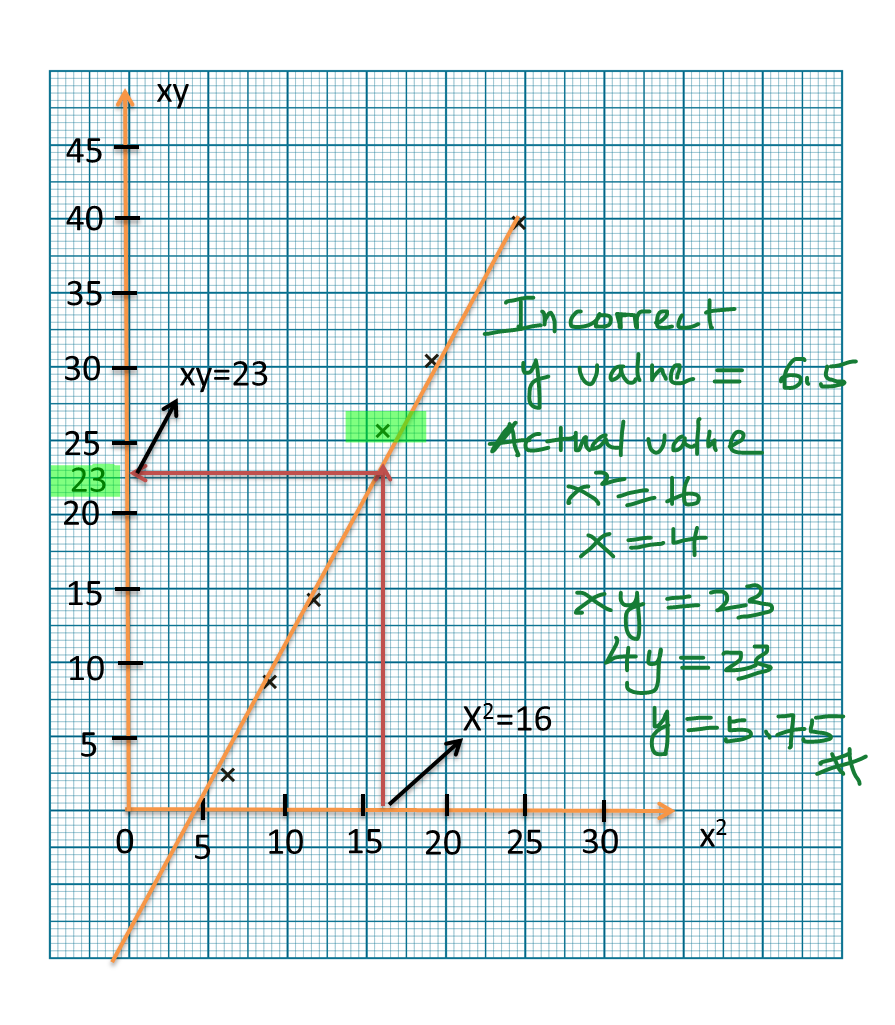
(b)(i) State the values of y which is incorrectly recorded and determine its actual value.
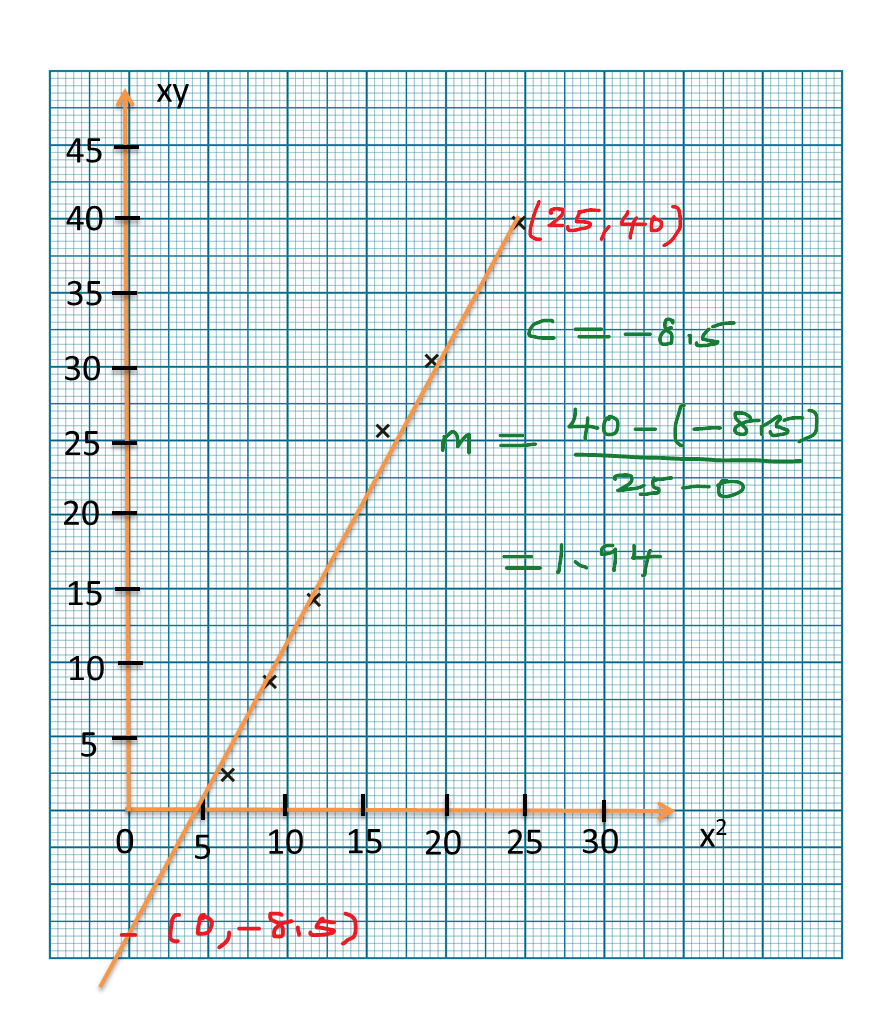
Step 3 : Calculate the gradient, m, and the Y-intercept, c, from the graph
Step 4 : Rewrite the original equation given and reduce it to linear form
Step 5 : Compare with the values of m and c obtained, find the values of the unknown required