7.5 Parallel Lines and Perpendicular Lines
(A) Parallel Lines
1. If two straight lines are parallel, they have same gradient.

Solution:
(A) Parallel Lines
1. If two straight lines are parallel, they have same gradient.

In the above diagram, if straight line L1 is parallel to straight line L2, gradient of L1 = gradient of L2
Example 1:
Given that the equation of a straight line parallel to x + 8y= 40 and passes through the point A(2, 3k) and B (-6, 4k2), find the values of k.
Solution:
(B) Perpendicular Lines
1. If two lines are perpendicular to each other, the product of their gradients is –1.
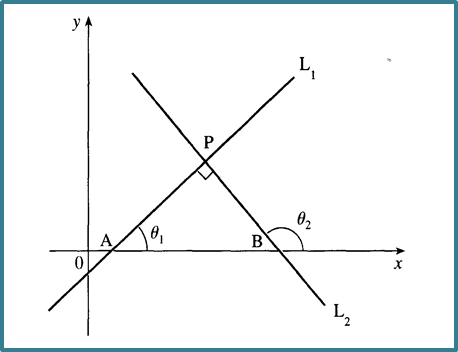
In the above diagram, if straight line L1 is perpendicular to straight line L2,
Example 2:
Hence, PQ is perpendicular to RS.
1. If two lines are perpendicular to each other, the product of their gradients is –1.

In the above diagram, if straight line L1 is perpendicular to straight line L2,
gradient of L1 × gradient of L2 = –1
Example 2:
Given that points P (–2, 4), Q (4, 2), R (–1, –3) and S (2, 6), show that PQ is perpendicular to RS.
Solution:
Hence, PQ is perpendicular to RS.