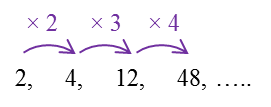5.4.1 Characteristics of a Geometry Progressions

2. Geometric Progression

(A) Characteristics of Geometric Progressions

Geometric progression is a progression in which the ratio of any term to the immediate term before is a constant. The constant is called common ratio, r.

Example:

Determine whether or not each of the following number sequences is a geometric progression (GP).

(a) 1, 4, 16, 64, …..

(b) 10, –5, 2.5, –1.25, …..

(c) 2, 4, 12, 48, …..

(d) –6, 1, 8, 15, …..

Solution:

[Smart Tips: For GP, times a fixed number every time to get the next time.]

(a)

\begin{array}{l} Common ratio, r = \frac{T_{n}}{T_{n - 1}} \\ \frac{T_{3}}{T_{2}} = \frac{16}{4} = 4, \frac{T_{2}}{T_{1}} = \frac{4}{1} = 4 \\ \frac{T_{3}}{T_{2}} = \frac{T_{2}}{T_{1}} \end{array}

This is a GP, a =1, r = 4.

(b)

\begin{array}{l} Common ratio, \\ r = \frac{T_{2}}{T_{1}} = - \frac{5}{10} = - \frac{1}{2} \end{array}

This is a GP, a =1, r = – ½.

(c)

This is NOT a GP.

This is because the ratio of each term to its preceding term is not a similar constant.

(B) The steps to prove whether a given number sequence is a geometric progression.

Step 1: List down any three consecutive terms. [Example: T₁, T₂, T₃.]

Step 2: Calculate the values of

\frac{T_{3}}{T_{2}} and \frac{T_{2}}{T_{1}} .

Step 3: If

\frac{T_{3}}{T_{2}} = \frac{T_{2}}{T_{1}} = r

, then the number sequence is a geometric
progression.

Step 4: If

\frac{T_{3}}{T_{2}} \neq \frac{T_{2}}{T_{1}}

, then the number sequence is not a geometric progression.

Leave a Comment Cancel reply