Question 13:
Solution:

Solution:

Question 14:
The quadratic equation has roots –2 and 6. Find
(a) the value of p and of q,
(b) the range of values of r for which the equation has no real roots.
Solution:
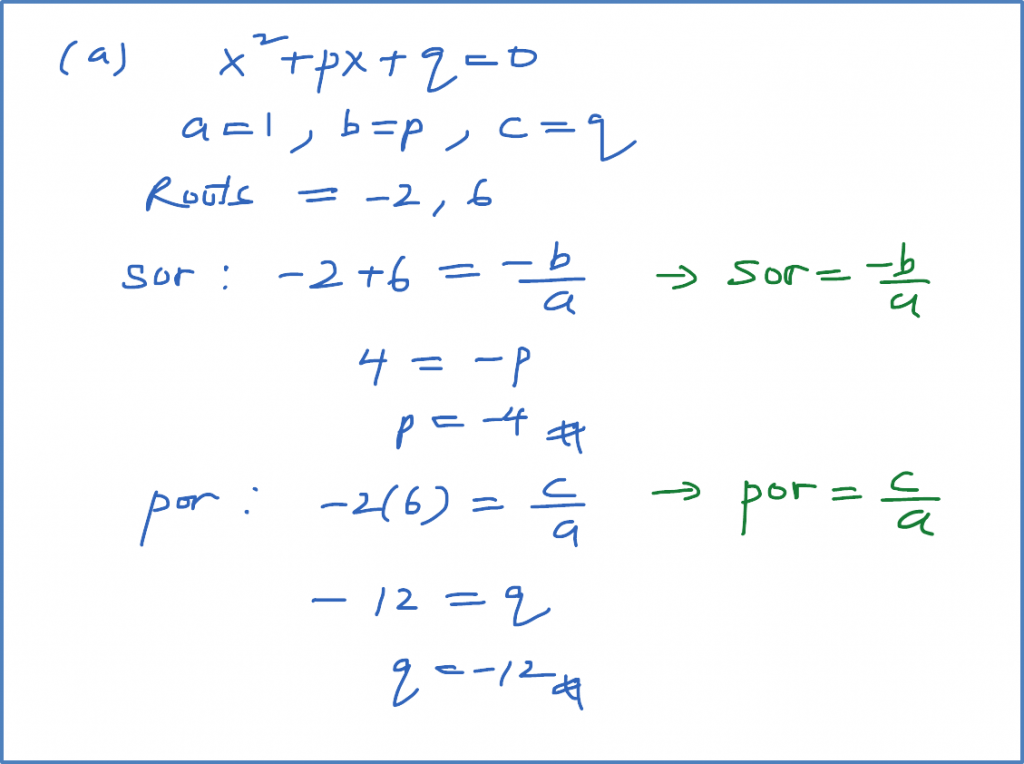

The quadratic equation has roots –2 and 6. Find
(a) the value of p and of q,
(b) the range of values of r for which the equation has no real roots.
Solution:
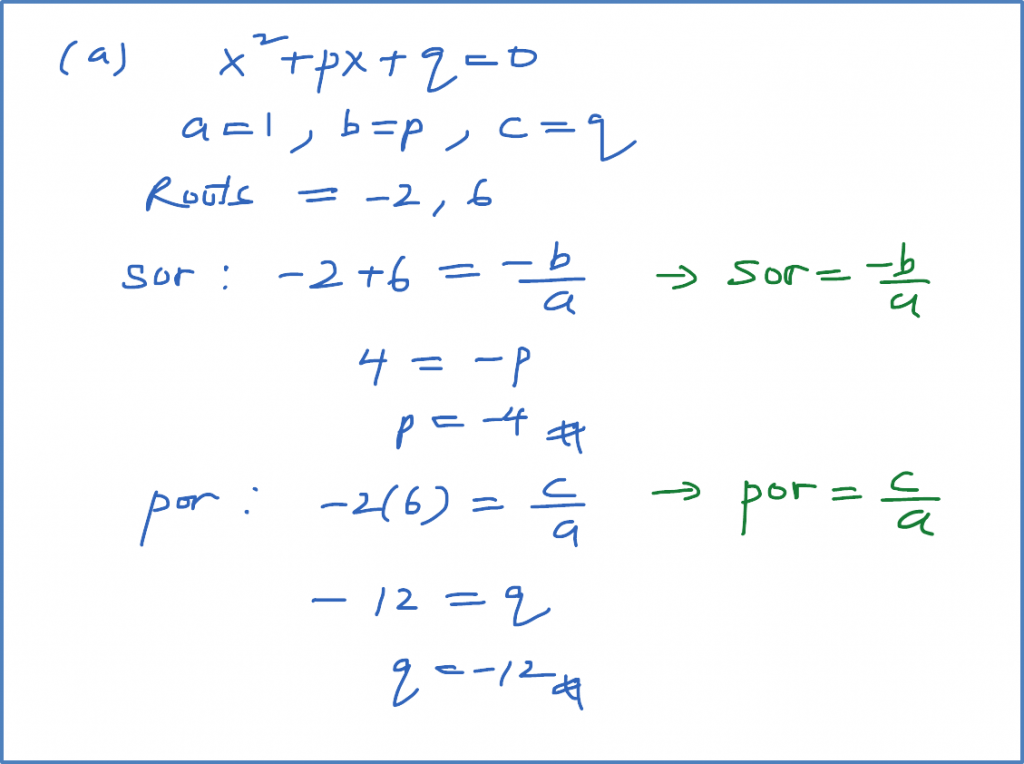

Question 15:
The straight line y = 5x – 1 does not intersect with the curve y = 2x2 + x + h.
Find the range of values of h.
Solution:
The straight line y = 5x – 1 does not intersect with the curve y = 2x2 + x + h.
Find the range of values of h.
Solution:
Question 16:
Find the range of values of p for which the equation has two real distinct roots.
Solution:

Find the range of values of p for which the equation has two real distinct roots.
Solution:
