Example 4:
(a) If f : x → x – 2, find f -1 (5),
(a) If f : x → x – 2, find f -1 (5),
(b) if f:x→x+9x−5, x≠5, find f−1(3).
Solution:
(a)
f (x) = x– 2
Let y = f -1 (5)
f (y) = 5
y – 2 = 5
y = 7
therefore, f -1 (5) = 7
(b)
f(x)=x+9x−5Let y=f−1(3)f(y)=3y+9y−5=3y+9=3y−152y=24y=12∴f−1(3)=12
Example 5
If g:x↦m−xx−3,x≠3 and g−1(5)=14 . Find the value of m.
Correction:
m – 14 = 55
m = 55 + 14
m = 69
If g:x↦m−xx−3,x≠3 and g−1(5)=14 . Find the value of m.
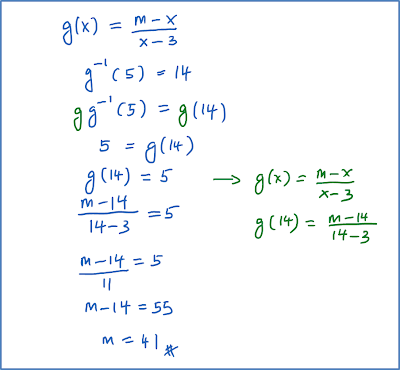Correction:
m – 14 = 55
m = 55 + 14
m = 69
Example 6 (Comparison Method)
If f:x↦mx−nx−2,x≠2 and f−1:x↦5−2x2−x,x≠2. . Find the value of m and of n,
If f:x↦mx−nx−2,x≠2 and f−1:x↦5−2x2−x,x≠2. . Find the value of m and of n,
the final answer of b is 12 right？
Dear Aini,
Thanks for pointing out our mistake.
Correction was done accordingly.