Question 10 (10 marks):
(a) Prove that 2 tan x cos2 x = sin 2x.
(b) Hence, solve the equation 4 tan x cos2 x = 1 for 0 ≤ x ≤ 2π.
(c)(i) Sketch the graph of y = sin 2x for 0 ≤ x ≤ 2π.
(c)(ii) Hence, using the same axes, sketch a suitable straight line to find the number of solutions for the equation 4π tan x cos2 x = x – 2π for 0 ≤ x ≤ 2π.
State the number of solutions.
Solution:
(a)
(b)
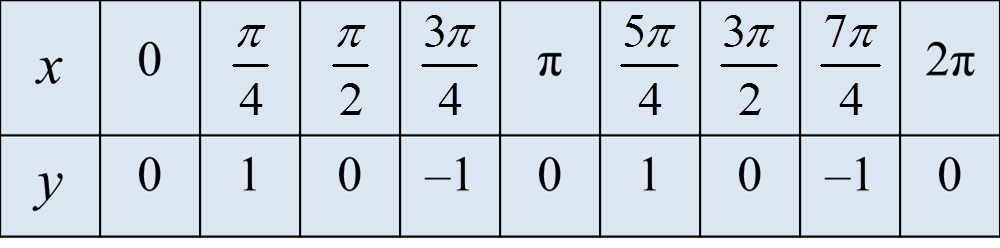
(c)(i)
y = sin 2x, 0 ≤ x ≤ 2π.
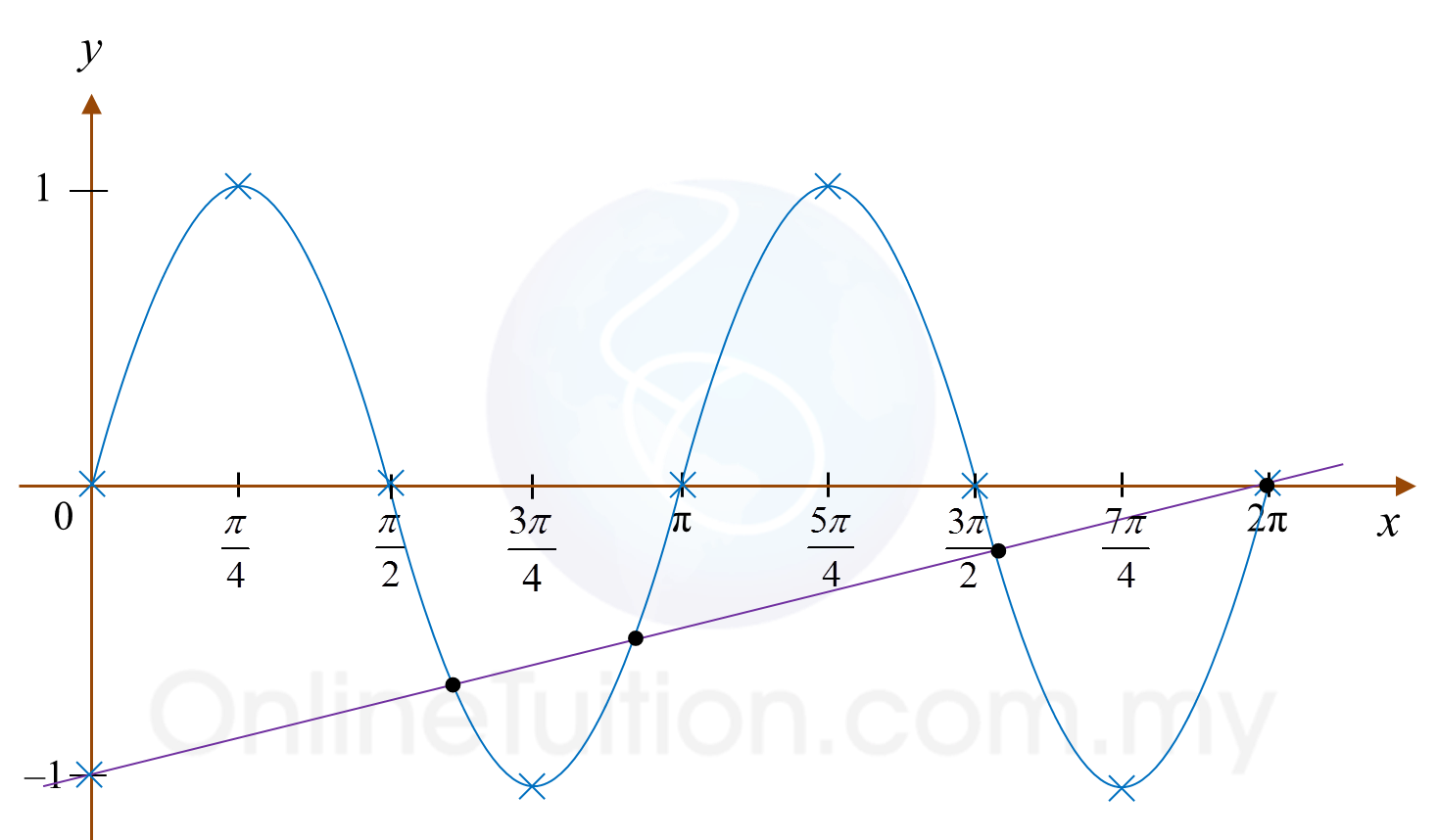
(c)(ii)
Number of solutions = 4
(a) Prove that 2 tan x cos2 x = sin 2x.
(b) Hence, solve the equation 4 tan x cos2 x = 1 for 0 ≤ x ≤ 2π.
(c)(i) Sketch the graph of y = sin 2x for 0 ≤ x ≤ 2π.
(c)(ii) Hence, using the same axes, sketch a suitable straight line to find the number of solutions for the equation 4π tan x cos2 x = x – 2π for 0 ≤ x ≤ 2π.
State the number of solutions.
Solution:
(a)
(b)

(c)(i)
y = sin 2x, 0 ≤ x ≤ 2π.


(c)(ii)

Number of solutions = 4
Question 11 (10 marks):
Diagram 6 shows a curve y = 2x2 – 18 and the straight line PQ which is a tangent to the curve at point K.
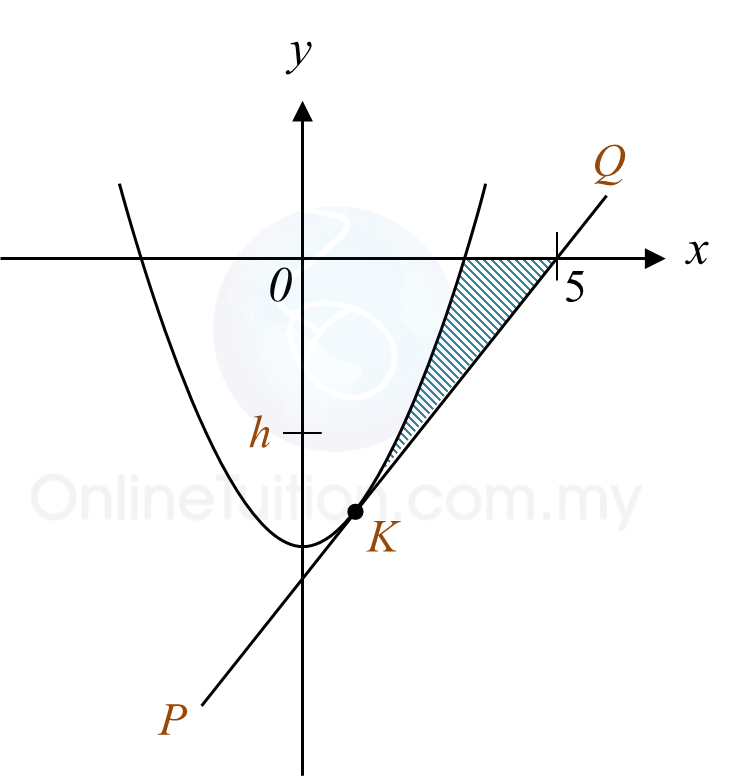
It is given that the gradient of the straight line PQ is 4.
(a) Find the coordinates of point K
(b) Calculate the area of the shaded region.
(c) When the region bounded by the curve, the x-axis and the straight line y = h is rotated through 180o about the y-axis, the volume generated is 65π unit3.
Find the value of h.
Solution:
(a)
(b)
(c)
Diagram 6 shows a curve y = 2x2 – 18 and the straight line PQ which is a tangent to the curve at point K.

It is given that the gradient of the straight line PQ is 4.
(a) Find the coordinates of point K
(b) Calculate the area of the shaded region.
(c) When the region bounded by the curve, the x-axis and the straight line y = h is rotated through 180o about the y-axis, the volume generated is 65π unit3.
Find the value of h.
Solution:
(a)
(b)
(c)