\

7.6.2 Probability, Long Questions (Question 2 & 3)


Question 2:
A bag contains 4 red cards, 6 blue cards and 5 green cards. A card is drawn at random and its colour is recorded and then it is returned to the bag before the second card is drawn at random. Find the probability that
(a) all the three cards are blue,
(b) there are two blue cards followed by one red card,
(c) the sequence of the cards drawn is red, green and blue,
(d) all the three cards have the same colour.

Solution:
Let R = red card, B = blue card, G = green card

(a)
Probability (all the three cards are blue ) = 6 15 × 6 15 × 6 15 = 8 125

(b)
Probability (two blue cards followed by one red card ) = 6 15 × 6 15 × 4 15 = 16 375

(c)
Probability (the sequence of the cards drawn is red, green and blue ) = 4 15 × 6 15 × 5 15 = 8 225

(d)
Probability (all the three cards have the same colour ) = P ( R R R ) + P ( B B B ) + P ( G G G ) = ( 4 15 ) 3 + ( 6 15 ) 3 + ( 5 15 ) 3 = 64 3375 + 216 3375 + 125 3375 = 3 25


Question 3:
A bag contains 4 blue beads, 3 red beads and 7 green beads. Two beads are drawn at random from the bag, one after the other without replacement. Find the probability that
(a) both the beads are of the same colour,
(b) both the beads are of different colours. 

Solution:





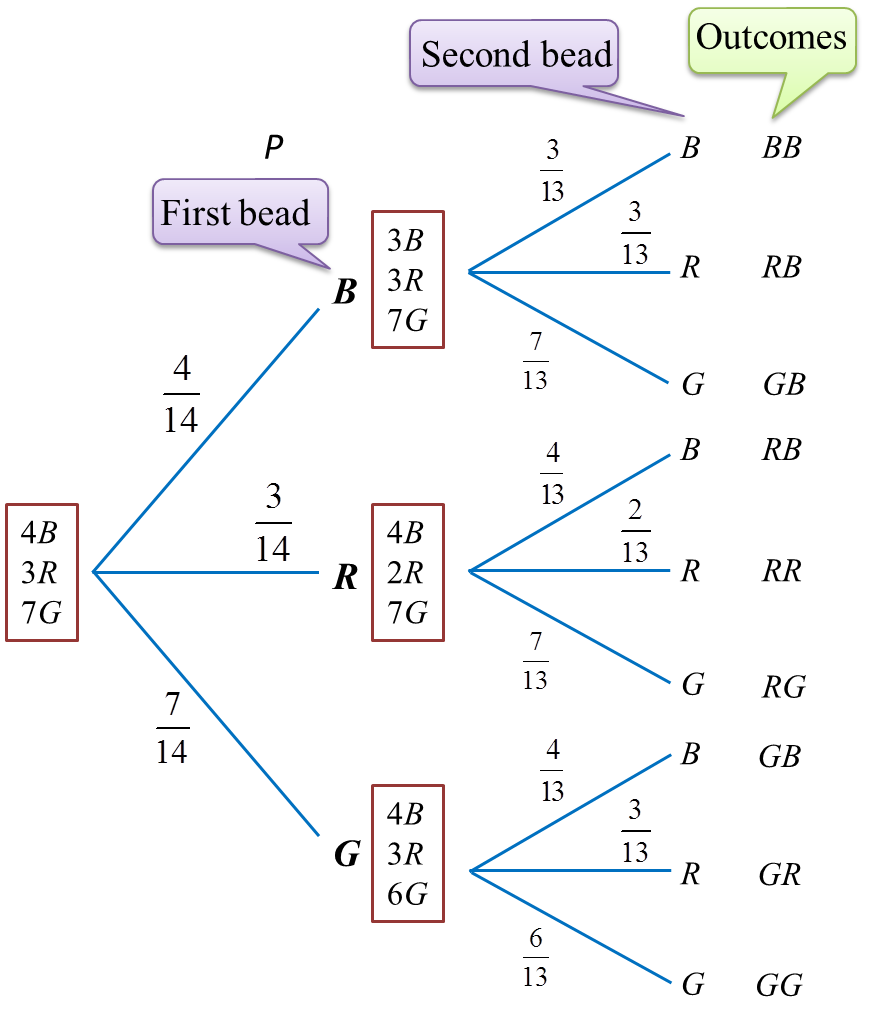
(a)
Probability (both the beads are of the same colour) =P( blue, blue )+P( red, red )+P( green, green ) =( 4 14 × 3 13 )+( 3 14 × 2 13 )+( 7 14 × 6 13 ) = 6 91 + 3 91 + 3 13 = 30 91

(b)
Probability (both the beads are of different colour ) = 1 − P ( both the beads are of the same colour ) = 1 − 30 91 ← From part (a) = 61 91

Leave a Comment