Question 7:
Diagram 3 shows a shape formed by a combination of four sectors and a square ABCD.
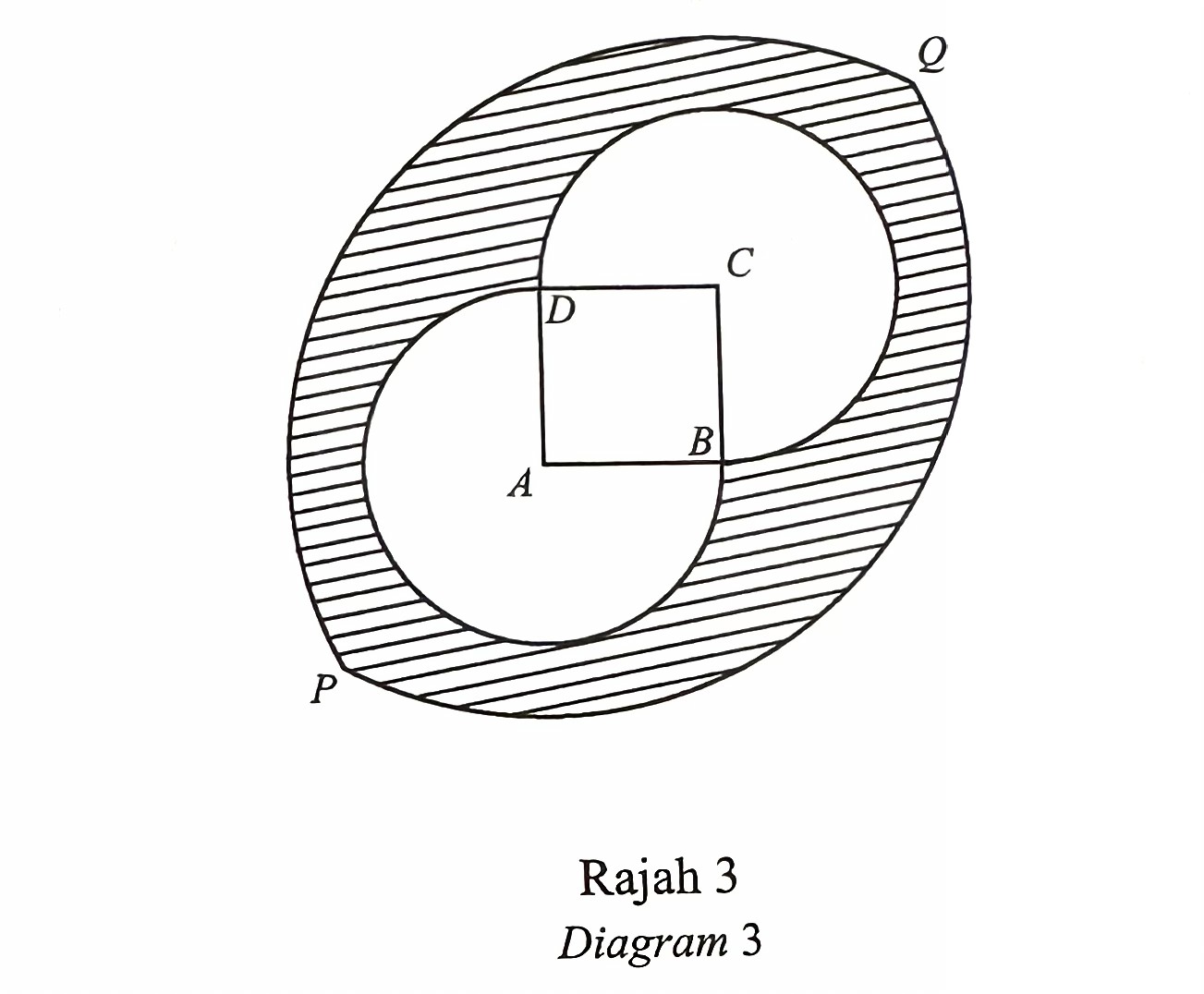A, B, C and D are the centres of sectors BAD, PBQ, BCD and PDQ. respectively. It is given that AB = 5 cm and the length of the straight line PQ which passes through points A and C is 23 cm.
[Use π = 3.142]
(a) Find ∠PBQ in radians, correct to two decimal places. [2 marks]
(b) Hence, find
(i) the outside perimeter, in cm,
(ii) the area, in cm2, of the shaded region.
[7 marks]
Answer:
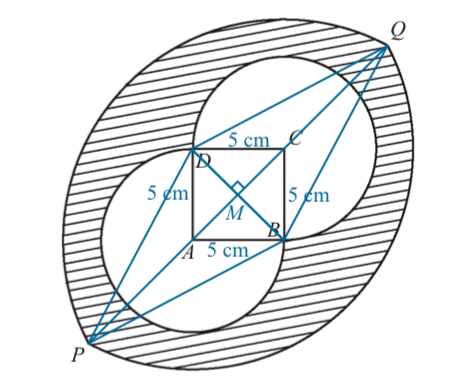
(a)
$$ \begin{aligned} P M=M Q & =\frac{1}{2} P Q=11.5 \mathrm{~cm} \\ B M=D M & =\frac{1}{2} B D \\ & =\frac{1}{2}\left(\sqrt{5^2+5^2}\right) \end{aligned} $$$$ \begin{aligned} & =\frac{1}{2}(5 \sqrt{2}) \\ & =\frac{5 \sqrt{2}}{2} \end{aligned} $$
$$ \begin{aligned} \angle P B Q & =2 \times \angle Q B M \\ & =2 \tan ^{-1}\left(\frac{Q M}{B M}\right) \\ & =2 \tan ^{-1}\left(\frac{11.5}{\frac{5 \sqrt{2}}{2}}\right) \\ & =2\left(72.91^{\circ}\right) \\ & =145.82^{\circ} \\ & =2.55 \mathrm{rad} \end{aligned} $$
(b)(i)
$$ \begin{aligned} B Q & =\sqrt{M Q^2+B M^2} \\ & =\sqrt{(11.5)^2+\left(\frac{5 \sqrt{2}}{2}\right)^2} \\ & =\sqrt{\frac{579}{4}} \\ & =12.0312 \mathrm{~cm} \end{aligned} $$
$$ \begin{aligned} &\text { Outside perimeter }=2 A B\\ &\begin{aligned} & =2 \times r \theta \\ & =2(12.0312)(2.55) \\ & =61.3591 \mathrm{~cm} \end{aligned} \end{aligned} $$
(b)(ii)
$$ \begin{aligned} & \text { Area of segment } P Q\\ &\begin{aligned} & =\frac{1}{2} r^2 \theta-\frac{1}{2} r^2 \sin \theta \\ & =\frac{1}{2}(12.0312)^2(2.55)-\frac{1}{2}(12.0312)^2 \sin 145.82^{\circ} \end{aligned} \end{aligned} $$= 184.5560 – 40.6598
= 143.8962 cm2
Area of whole diagram = 2 × 143.8962 = 287.7924 cm2
$$ \begin{aligned} &\text { Area of sector } B C D \\ &\begin{aligned} & =\frac{1}{2}(5)^2\left(\frac{3 \pi}{2}\right) \\ & =58.9125 \mathrm{~cm}^2 \end{aligned} \end{aligned} $$
Luas kawasan berlorek
= Area of whole diagram – Area of sector BCD – Area of sector BAD – Area of ABCD
= 287.7924 – 58.9125 – 58.9125 – (5 × 5)
= 144.9674 cm2
Diagram 3 shows a shape formed by a combination of four sectors and a square ABCD.
A, B, C and D are the centres of sectors BAD, PBQ, BCD and PDQ. respectively. It is given that AB = 5 cm and the length of the straight line PQ which passes through points A and C is 23 cm.[Use π = 3.142]
(a) Find ∠PBQ in radians, correct to two decimal places. [2 marks]
(b) Hence, find
(i) the outside perimeter, in cm,
(ii) the area, in cm2, of the shaded region.
[7 marks]
Answer:
(a)
$$ \begin{aligned} P M=M Q & =\frac{1}{2} P Q=11.5 \mathrm{~cm} \\ B M=D M & =\frac{1}{2} B D \\ & =\frac{1}{2}\left(\sqrt{5^2+5^2}\right) \end{aligned} $$$$ \begin{aligned} & =\frac{1}{2}(5 \sqrt{2}) \\ & =\frac{5 \sqrt{2}}{2} \end{aligned} $$
$$ \begin{aligned} \angle P B Q & =2 \times \angle Q B M \\ & =2 \tan ^{-1}\left(\frac{Q M}{B M}\right) \\ & =2 \tan ^{-1}\left(\frac{11.5}{\frac{5 \sqrt{2}}{2}}\right) \\ & =2\left(72.91^{\circ}\right) \\ & =145.82^{\circ} \\ & =2.55 \mathrm{rad} \end{aligned} $$
(b)(i)
$$ \begin{aligned} B Q & =\sqrt{M Q^2+B M^2} \\ & =\sqrt{(11.5)^2+\left(\frac{5 \sqrt{2}}{2}\right)^2} \\ & =\sqrt{\frac{579}{4}} \\ & =12.0312 \mathrm{~cm} \end{aligned} $$
$$ \begin{aligned} &\text { Outside perimeter }=2 A B\\ &\begin{aligned} & =2 \times r \theta \\ & =2(12.0312)(2.55) \\ & =61.3591 \mathrm{~cm} \end{aligned} \end{aligned} $$
(b)(ii)
$$ \begin{aligned} & \text { Area of segment } P Q\\ &\begin{aligned} & =\frac{1}{2} r^2 \theta-\frac{1}{2} r^2 \sin \theta \\ & =\frac{1}{2}(12.0312)^2(2.55)-\frac{1}{2}(12.0312)^2 \sin 145.82^{\circ} \end{aligned} \end{aligned} $$= 184.5560 – 40.6598
= 143.8962 cm2
Area of whole diagram = 2 × 143.8962 = 287.7924 cm2
$$ \begin{aligned} &\text { Area of sector } B C D \\ &\begin{aligned} & =\frac{1}{2}(5)^2\left(\frac{3 \pi}{2}\right) \\ & =58.9125 \mathrm{~cm}^2 \end{aligned} \end{aligned} $$
Luas kawasan berlorek
= Area of whole diagram – Area of sector BCD – Area of sector BAD – Area of ABCD
= 287.7924 – 58.9125 – 58.9125 – (5 × 5)
= 144.9674 cm2