Question 14:
Julie produces two types of dolls, Mal and Tod. Table 3 shows information regarding the dolls produced.
The dolls produced by Julie satisfy the following constraints:
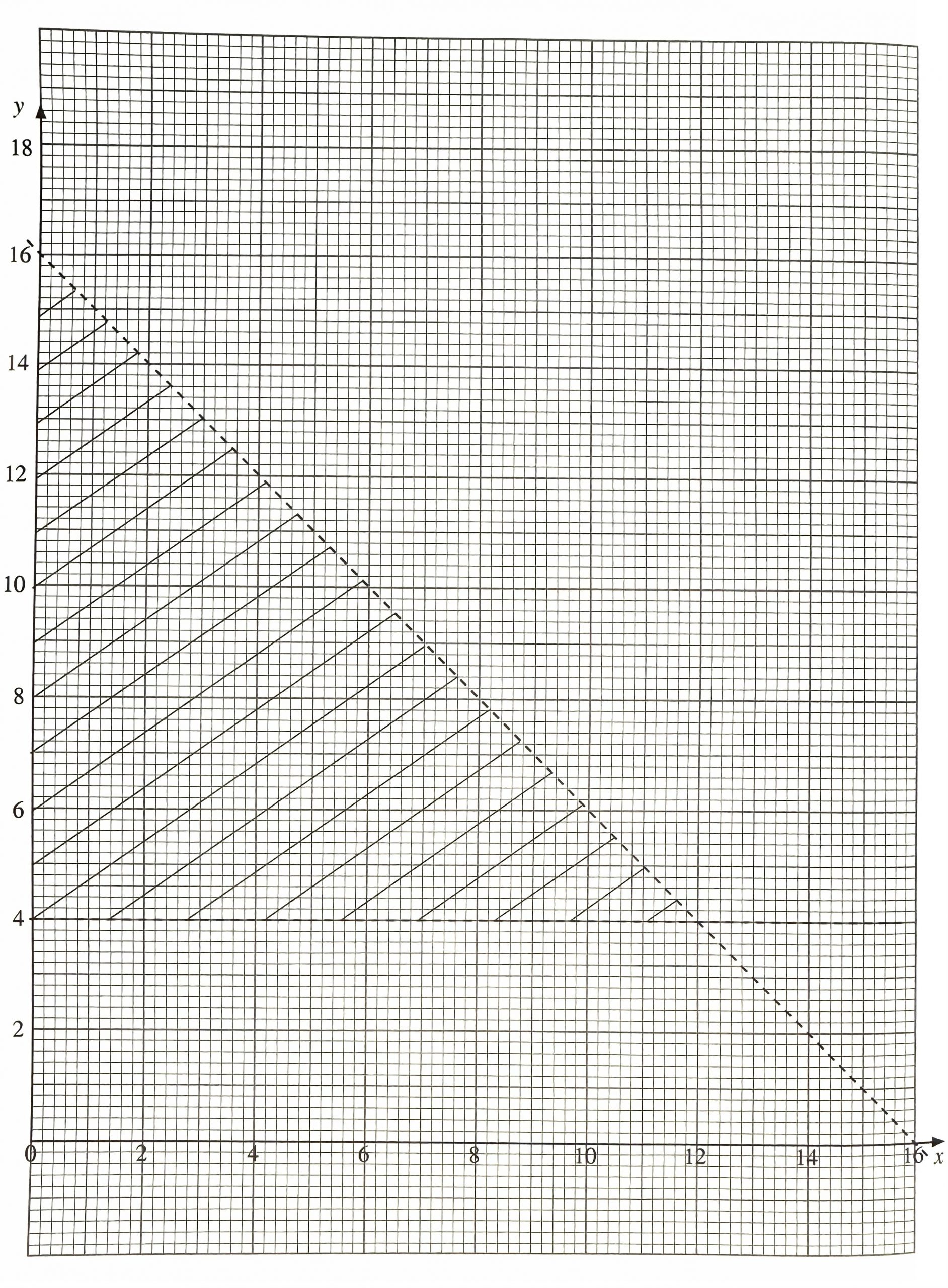
(a) Constraints I and II are shown on the graph on page 116. The shaded region represents the points which satisfy the both constraints.
State the value of p and of q.
[1 mark]
(b) Write an inequality for constraint III, other than x ≥ 0 and y ≥ 0.
Hence, on page 116, construct and label the region R which satisfies all the constraints.
[3 marks]
(c) Use the graph constructed in (b) to answer the following question:
(i) On a particular day, the ratio of the number of Tod dolls to the number of Mal dolls produced is 3 : 2.
Determine the possible numbers of Mal dolls produced on that day.
(ii) Given that the total cost to produce the Mal dolls and Tod dolls is RM k, express k in terms of x and y.
Hence, draw the objective function and find the maximum cost.
[6 marks]
Answer:
Answer:
(a) p = 16, q = 4
(b) y ≤ 2x

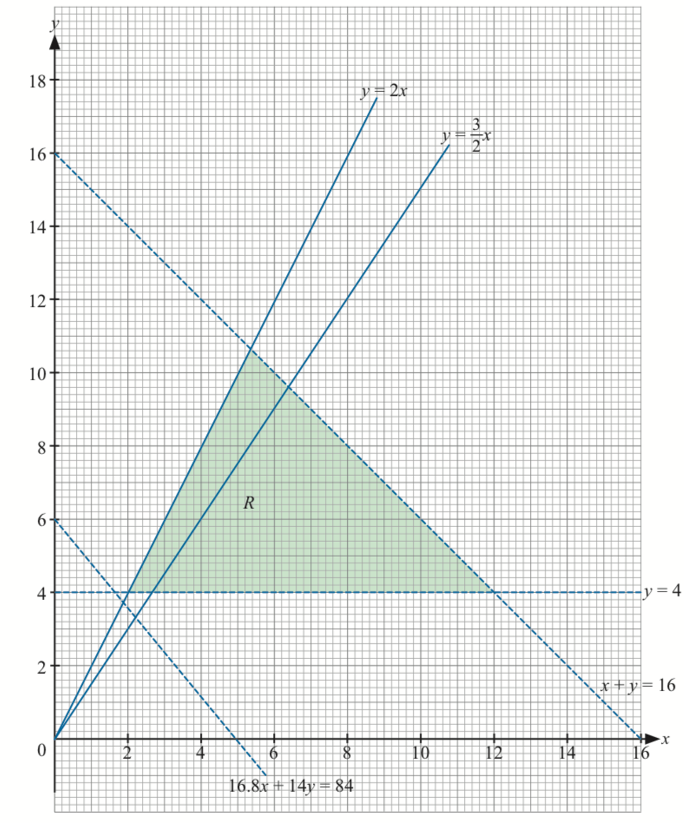
(c)(i)
Method 1 = Algebraic method

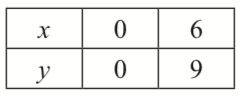
Method 2 = Graphical method $$ \begin{aligned} & \frac{y}{x}=\frac{3}{2} \\ & y=\frac{3}{2} x \end{aligned} $$
∴ Possible number of Mal’s dolls are 4 and 6 .
(c)(ii)
$$ \begin{aligned} &k=16.8 x+14 y\\ &\text { Let } 16.8 x+14 y=84 \end{aligned} $$
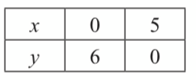
$$ \text { Maximum point }=(12,4) $$
$$ \begin{aligned} \text { Maximum cost } & =16.8(12)+14(4) \\ & =\mathrm{RM} 257.60 \end{aligned} $$
Julie produces two types of dolls, Mal and Tod. Table 3 shows information regarding the dolls produced.

The dolls produced by Julie satisfy the following constraints:
| I : The total number of Mal and Tod dolls produced is less than p units. II : The number of Tod dolls produced is more than q units. III : The number of Tod dolls produced is not more than 2 times the number of Mal dolls. |
State the value of p and of q.
[1 mark]
(b) Write an inequality for constraint III, other than x ≥ 0 and y ≥ 0.
Hence, on page 116, construct and label the region R which satisfies all the constraints.
[3 marks]
(c) Use the graph constructed in (b) to answer the following question:
(i) On a particular day, the ratio of the number of Tod dolls to the number of Mal dolls produced is 3 : 2.
Determine the possible numbers of Mal dolls produced on that day.
(ii) Given that the total cost to produce the Mal dolls and Tod dolls is RM k, express k in terms of x and y.
Hence, draw the objective function and find the maximum cost.
[6 marks]
Answer:

Answer:
(a) p = 16, q = 4
(b) y ≤ 2x


(c)(i)
Method 1 = Algebraic method

Method 2 = Graphical method $$ \begin{aligned} & \frac{y}{x}=\frac{3}{2} \\ & y=\frac{3}{2} x \end{aligned} $$

∴ Possible number of Mal’s dolls are 4 and 6 .
(c)(ii)
$$ \begin{aligned} &k=16.8 x+14 y\\ &\text { Let } 16.8 x+14 y=84 \end{aligned} $$

$$ \text { Maximum point }=(12,4) $$
$$ \begin{aligned} \text { Maximum cost } & =16.8(12)+14(4) \\ & =\mathrm{RM} 257.60 \end{aligned} $$