Question 10:
Solutions by scale drawing and vector are not accepted.
Diagram 5 shows four points A, B, C and D on a Cartesian plane.

(a) It is given that points B, C and D are collinear such that BC : CD = 1 : 3.
(i) Find the coordinates of D in terms of h.
(ii) Hence, calculate the value of h if the area of ΔACD is 27 units2.
[4 marks]
(b)(i) P(x, y) moves such that its distance from point B and point D are equal.
Using the distance formula, find the equation of the locus of P.
(ii) Locus P intersects the y-axis at point E.
Determine whether the straight lines BA and CE are parallel or not.
[6 marks]
Answer:
(a)(i)
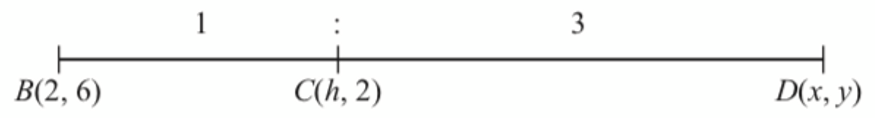
$$ \begin{aligned} C(h, 2) & =\left(\frac{3(2)+(1)(x)}{1+3}, \frac{(3)(6)+(1)(y)}{1+3}\right) \\ & =\left(\frac{6+x}{4}, \frac{18+y}{4}\right) \end{aligned} $$
$$ \begin{aligned} \frac{6+x}{4} & =h \\ 6+x & =4 h \\ x & =4 h-6 \end{aligned} $$
$$ \begin{aligned} \frac{18+y}{4} & =2 \\ 18+y & =8 \\ y & =8-18 \\ y & =-10 \end{aligned} $$
$$ \therefore D(4 h-6,-10) $$
(a)(ii)
$$ \begin{aligned} &\text { Area of } \triangle A C D=27 \text { unit }^2\\ &\frac{1}{2}\left|\begin{array}{cccc} -1 & h & 4 h-6 & -1 \\ 0 & 2 & -10 & 0 \end{array}\right|=27 \end{aligned} $$$$ \left|\begin{array}{c} {[(-1)(2)+(h)(-10)+(0)(4 h-6)} \\ -[(0)(h)+(2)(4 h-6)+(-10)(-1) \end{array}\right|=54 $$$$ \begin{aligned} |(-2-10 h)-(8 h-12+10)| & =54 \\ |-2-10 h-8 h+12-10| & =54 \\ |-18 h| & =54 \end{aligned} $$
$$ \begin{aligned} -18 h & =54 \\ h & =-3(\text { ignore }) \end{aligned} $$
$$ \begin{aligned} -(-18 h) & =54 \\ h & =3 \end{aligned} $$$$ \therefore h=3 $$
(b)(i)
$$ \begin{aligned} & D(4 h-6,-10) \text { when } h=3 \\ & \therefore D(6,-10) \end{aligned} $$
$$ \begin{aligned} B P & =P D \\ \sqrt{(2-x)^2+(6-y)^2} & =\sqrt{(6-x)^2+(-10-y)^2} \\ \sqrt{x^2-4 x+4+y^2-12 y+36} & =\sqrt{x^2-12 x+36+y^2+20 y+100} \\ x^2+y^2-4 x-12 y+40 & =x^2+y^2-12 x+20 y+136 \\ -4 x+12 x-12 y-20 y+40-136 & =0 \\ 8 x-32 y-96 & =0 \end{aligned} $$
(b)(ii)
$$ \text { Intersection of } y \text {-axis, } x=0 $$
$$ \begin{aligned} 8 x-32 y-96 & =0 \\ 8(0)-32 y-96 & =0 \\ -32 y & =96 \\ y & =-3 \end{aligned} $$$$ \therefore E(0,-3) $$
$$ \begin{aligned} & m_{B A}=\frac{6-0}{2-(-1)}=2 \\ & m_{C E}=\frac{-3-2}{0-3}=\frac{5}{3} \\ & m_{B A} \neq m_{C E} \end{aligned} $$
∴ BA is not parallel to CE.
Solutions by scale drawing and vector are not accepted.
Diagram 5 shows four points A, B, C and D on a Cartesian plane.

(a) It is given that points B, C and D are collinear such that BC : CD = 1 : 3.
(i) Find the coordinates of D in terms of h.
(ii) Hence, calculate the value of h if the area of ΔACD is 27 units2.
[4 marks]
(b)(i) P(x, y) moves such that its distance from point B and point D are equal.
Using the distance formula, find the equation of the locus of P.
(ii) Locus P intersects the y-axis at point E.
Determine whether the straight lines BA and CE are parallel or not.
[6 marks]
Answer:
(a)(i)
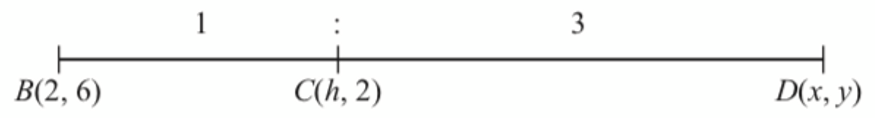
$$ \begin{aligned} C(h, 2) & =\left(\frac{3(2)+(1)(x)}{1+3}, \frac{(3)(6)+(1)(y)}{1+3}\right) \\ & =\left(\frac{6+x}{4}, \frac{18+y}{4}\right) \end{aligned} $$
$$ \begin{aligned} \frac{6+x}{4} & =h \\ 6+x & =4 h \\ x & =4 h-6 \end{aligned} $$
$$ \begin{aligned} \frac{18+y}{4} & =2 \\ 18+y & =8 \\ y & =8-18 \\ y & =-10 \end{aligned} $$
$$ \therefore D(4 h-6,-10) $$
(a)(ii)
$$ \begin{aligned} &\text { Area of } \triangle A C D=27 \text { unit }^2\\ &\frac{1}{2}\left|\begin{array}{cccc} -1 & h & 4 h-6 & -1 \\ 0 & 2 & -10 & 0 \end{array}\right|=27 \end{aligned} $$$$ \left|\begin{array}{c} {[(-1)(2)+(h)(-10)+(0)(4 h-6)} \\ -[(0)(h)+(2)(4 h-6)+(-10)(-1) \end{array}\right|=54 $$$$ \begin{aligned} |(-2-10 h)-(8 h-12+10)| & =54 \\ |-2-10 h-8 h+12-10| & =54 \\ |-18 h| & =54 \end{aligned} $$
$$ \begin{aligned} -18 h & =54 \\ h & =-3(\text { ignore }) \end{aligned} $$
$$ \begin{aligned} -(-18 h) & =54 \\ h & =3 \end{aligned} $$$$ \therefore h=3 $$
(b)(i)
$$ \begin{aligned} & D(4 h-6,-10) \text { when } h=3 \\ & \therefore D(6,-10) \end{aligned} $$
$$ \begin{aligned} B P & =P D \\ \sqrt{(2-x)^2+(6-y)^2} & =\sqrt{(6-x)^2+(-10-y)^2} \\ \sqrt{x^2-4 x+4+y^2-12 y+36} & =\sqrt{x^2-12 x+36+y^2+20 y+100} \\ x^2+y^2-4 x-12 y+40 & =x^2+y^2-12 x+20 y+136 \\ -4 x+12 x-12 y-20 y+40-136 & =0 \\ 8 x-32 y-96 & =0 \end{aligned} $$
(b)(ii)
$$ \text { Intersection of } y \text {-axis, } x=0 $$
$$ \begin{aligned} 8 x-32 y-96 & =0 \\ 8(0)-32 y-96 & =0 \\ -32 y & =96 \\ y & =-3 \end{aligned} $$$$ \therefore E(0,-3) $$
$$ \begin{aligned} & m_{B A}=\frac{6-0}{2-(-1)}=2 \\ & m_{C E}=\frac{-3-2}{0-3}=\frac{5}{3} \\ & m_{B A} \neq m_{C E} \end{aligned} $$
∴ BA is not parallel to CE.