Question 8:
Listing out all terms of the sequence is not accepted.
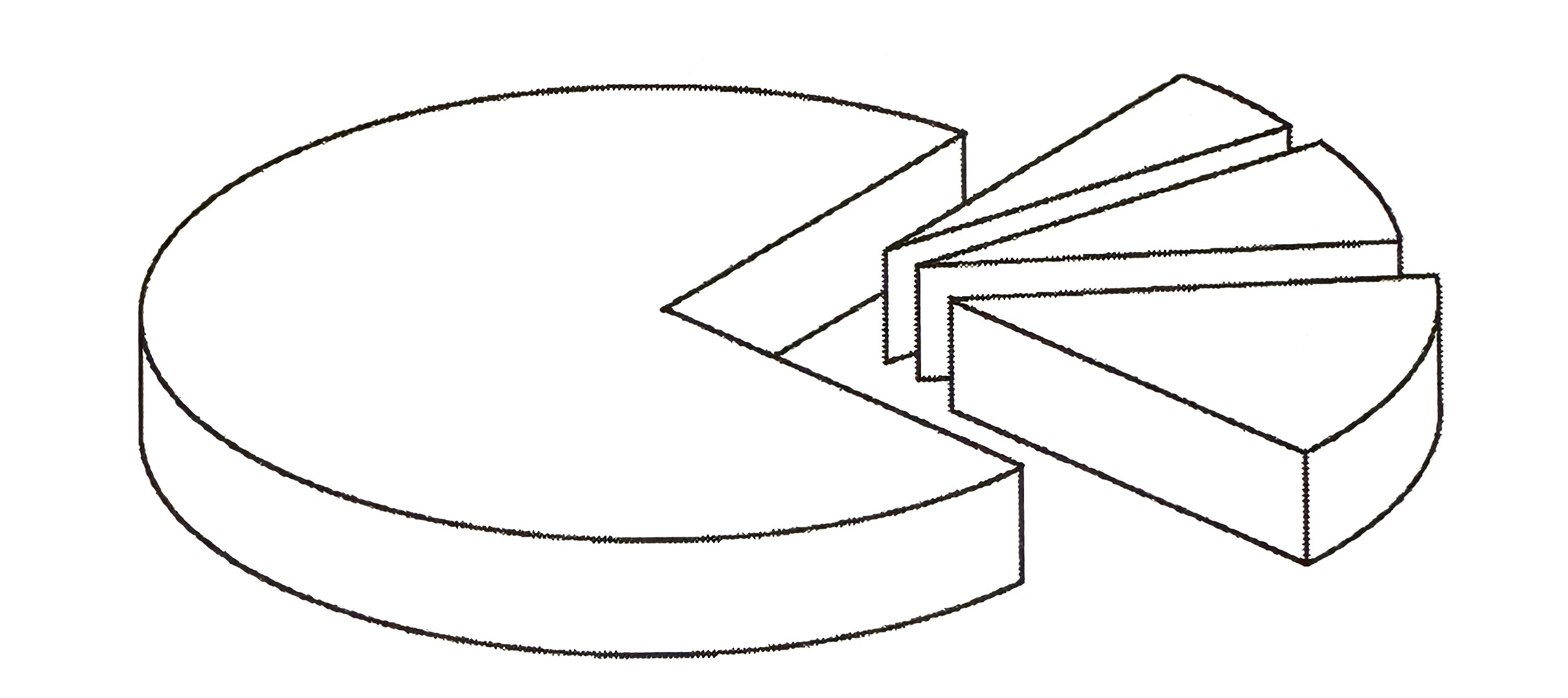
A cylindrical wooden block is cut into pieces for decoration purposes. Diagram 7 shows the first three pieces that have been cut and the remaining part.
The angles of the sectors increase by a constant amount for each subsequent piece. A total of n pieces can be cut from this block. The angle of sector of the 4th piece is 3 times the angle of sector of the smallest piece. The sum of the angles of the sectors for the first 4 pieces is 72∘.
(a) the angle of the sector, in degrees, for the smallest piece, [4 marks]
(b) the value of n. [3 marks]
Solution:
(a)
$$ \begin{aligned} &\text { Arithmetic progression, }\\ &\begin{aligned} T_n & =a+(n-1) d \\ S_n & =\frac{n}{2}[2 a+(n-1) d] \end{aligned} \end{aligned} $$
$$ \begin{aligned} T_4 & =3 T_1 \\ a+(4-1)(d) & =3 a \\ a+3 d & =3 a \\ 3 d & =2 a \ldots(1) \end{aligned} $$
$$ \begin{aligned} S_4 & =72^{\circ} \\ \frac{4}{2}[2 a+(4-1)(d)] & =72^{\circ} \\ 2(2 a+3 d) & =72^{\circ} \\ 2(2 a+2 a) & =72^{\circ} \\ 8 a & =72^{\circ} \\ a & =9^{\circ} \\ \text { Smallest piece }=T_1 & =a=9^{\circ} \end{aligned} $$
(b)
$$ \text { From (1), } \begin{aligned} 3 d & =2(9) \\ 3 d & =18 \\ d & =6 \end{aligned} $$
$$ \begin{aligned} & S_n=360^{\circ} \\ & \frac{n}{2}[2(9)+(n-1)(6)]=360^{\circ} \\ & \frac{n}{2}(18+6 n-6)=360^{\circ} \\ & n(6 n+12)=720^{\circ} \\ & 6 n^2+12 n-720^{\circ}=0 \\ & n^2+2 n-120^{\circ}=0 \\ &(n-10)(n+12)=0 \\ & n-10=0, n+12=0 \\ & n=10, n=-12 \text { (ignore) } \\ & \therefore n=10 \end{aligned} $$
Listing out all terms of the sequence is not accepted.

A cylindrical wooden block is cut into pieces for decoration purposes. Diagram 7 shows the first three pieces that have been cut and the remaining part.
The angles of the sectors increase by a constant amount for each subsequent piece. A total of n pieces can be cut from this block. The angle of sector of the 4th piece is 3 times the angle of sector of the smallest piece. The sum of the angles of the sectors for the first 4 pieces is 72∘.
(a) the angle of the sector, in degrees, for the smallest piece, [4 marks]
(b) the value of n. [3 marks]
Solution:
(a)
$$ \begin{aligned} &\text { Arithmetic progression, }\\ &\begin{aligned} T_n & =a+(n-1) d \\ S_n & =\frac{n}{2}[2 a+(n-1) d] \end{aligned} \end{aligned} $$
$$ \begin{aligned} T_4 & =3 T_1 \\ a+(4-1)(d) & =3 a \\ a+3 d & =3 a \\ 3 d & =2 a \ldots(1) \end{aligned} $$
$$ \begin{aligned} S_4 & =72^{\circ} \\ \frac{4}{2}[2 a+(4-1)(d)] & =72^{\circ} \\ 2(2 a+3 d) & =72^{\circ} \\ 2(2 a+2 a) & =72^{\circ} \\ 8 a & =72^{\circ} \\ a & =9^{\circ} \\ \text { Smallest piece }=T_1 & =a=9^{\circ} \end{aligned} $$
(b)
$$ \text { From (1), } \begin{aligned} 3 d & =2(9) \\ 3 d & =18 \\ d & =6 \end{aligned} $$
$$ \begin{aligned} & S_n=360^{\circ} \\ & \frac{n}{2}[2(9)+(n-1)(6)]=360^{\circ} \\ & \frac{n}{2}(18+6 n-6)=360^{\circ} \\ & n(6 n+12)=720^{\circ} \\ & 6 n^2+12 n-720^{\circ}=0 \\ & n^2+2 n-120^{\circ}=0 \\ &(n-10)(n+12)=0 \\ & n-10=0, n+12=0 \\ & n=10, n=-12 \text { (ignore) } \\ & \therefore n=10 \end{aligned} $$
Question 9:
$$ (a) \text { Given that } 2^x=8^y=\sqrt{2^{3 z}} \text {, find } x: y: z \text {. }{[2 marks]} $$
$$ (b) \text { Given that } 9^{2pq+1}+3^{4 pq-3}=732 \text {, express } p \text { in terms of } q \text {. }{[3 marks]} $$
$$ (c) \text { Find the value of } \frac{1}{\log _a a b}+\frac{1}{\log _b a b} \text {. }{[2 marks]} $$
Solution:
(a)
$$ \begin{aligned} 2 x^2 & =8 y=\sqrt{2^{3 z}} \\ 2^x & =\left(2^3\right) y=\left(2^{3 z}\right)^{\frac{1}{2}} \\ 2^x & =2^{3 y}=2^{\frac{3 x}{2}} \\ x & =3 y=\frac{3 z}{2} \end{aligned} $$
$$ \begin{aligned} & x=3 y \\ & \frac{x}{y}=\frac{3}{1} \\ & x: y=3: 1 \end{aligned} $$
$$ \begin{aligned} 3 y & =\frac{3 z}{2} \\ \frac{y}{z} & =\frac{3}{6} \\ \frac{y}{z} & =\frac{1}{2} \\ y: z & =1: 2 \end{aligned} $$
$$ \begin{aligned} & x: y: z \\ & 3: 1 \\ & \quad 1: 2 \\ & \therefore x: y: z=3: 1: 2 \end{aligned} $$
(b)
$$ \begin{aligned} 9^{2 p q+1}+3^{4 p q-3} & =732 \\ 3^{2(2 p q+1)}+3^{4 p q-3} & =732 \\ 3^{4 p q+2}+3^{4 p q-3} & =732 \\ \left(3^{4 p q}\right)\left(3^2\right)+\left(3^{4 p q}\right)\left(3^{-3}\right) & =732 \\ 3^{4 p q}\left(3^2+3^{-3}\right) & =732 \\ 3^{4 p q}\left(9+\frac{1}{27}\right) & =732 \\ 3^{4 p q}\left(\frac{244}{27}\right) & =732 \\ 3^{4 p q} & =732 \div \frac{244}{27} \\ 3^{4 p q} & =81 \\ 3^{4 p q} & =3^4 \\ 4 p q & =4 \\ p q & =1 \\ p & =\frac{1}{q} \end{aligned} $$
(c)
$$ \begin{aligned} & \frac{1}{\log _a a b}+\frac{1}{\log _b a b} \\ & =\frac{1}{\log _{a b} a b}+\frac{1}{\log _{a b} a}+\frac{\log _{a b} a b}{\log _{a b} b} \\ & =\frac{\log _{a b} a}{\log _{a b} a b}+\frac{\log _{a b} b}{\log _{a b} a b} \\ & =\frac{\log _{a b} a}{1}+\frac{\log _{a b} b}{1} \\ & =\log _{a b} a+\log _{a b} b \\ & =\log _{a b}(a \times b) \\ & =\log _{a b} a b \\ & =1 \end{aligned} $$
$$ (a) \text { Given that } 2^x=8^y=\sqrt{2^{3 z}} \text {, find } x: y: z \text {. }{[2 marks]} $$
$$ (b) \text { Given that } 9^{2pq+1}+3^{4 pq-3}=732 \text {, express } p \text { in terms of } q \text {. }{[3 marks]} $$
$$ (c) \text { Find the value of } \frac{1}{\log _a a b}+\frac{1}{\log _b a b} \text {. }{[2 marks]} $$
Solution:
(a)
$$ \begin{aligned} 2 x^2 & =8 y=\sqrt{2^{3 z}} \\ 2^x & =\left(2^3\right) y=\left(2^{3 z}\right)^{\frac{1}{2}} \\ 2^x & =2^{3 y}=2^{\frac{3 x}{2}} \\ x & =3 y=\frac{3 z}{2} \end{aligned} $$
$$ \begin{aligned} & x=3 y \\ & \frac{x}{y}=\frac{3}{1} \\ & x: y=3: 1 \end{aligned} $$
$$ \begin{aligned} 3 y & =\frac{3 z}{2} \\ \frac{y}{z} & =\frac{3}{6} \\ \frac{y}{z} & =\frac{1}{2} \\ y: z & =1: 2 \end{aligned} $$
$$ \begin{aligned} & x: y: z \\ & 3: 1 \\ & \quad 1: 2 \\ & \therefore x: y: z=3: 1: 2 \end{aligned} $$
(b)
$$ \begin{aligned} 9^{2 p q+1}+3^{4 p q-3} & =732 \\ 3^{2(2 p q+1)}+3^{4 p q-3} & =732 \\ 3^{4 p q+2}+3^{4 p q-3} & =732 \\ \left(3^{4 p q}\right)\left(3^2\right)+\left(3^{4 p q}\right)\left(3^{-3}\right) & =732 \\ 3^{4 p q}\left(3^2+3^{-3}\right) & =732 \\ 3^{4 p q}\left(9+\frac{1}{27}\right) & =732 \\ 3^{4 p q}\left(\frac{244}{27}\right) & =732 \\ 3^{4 p q} & =732 \div \frac{244}{27} \\ 3^{4 p q} & =81 \\ 3^{4 p q} & =3^4 \\ 4 p q & =4 \\ p q & =1 \\ p & =\frac{1}{q} \end{aligned} $$
(c)
$$ \begin{aligned} & \frac{1}{\log _a a b}+\frac{1}{\log _b a b} \\ & =\frac{1}{\log _{a b} a b}+\frac{1}{\log _{a b} a}+\frac{\log _{a b} a b}{\log _{a b} b} \\ & =\frac{\log _{a b} a}{\log _{a b} a b}+\frac{\log _{a b} b}{\log _{a b} a b} \\ & =\frac{\log _{a b} a}{1}+\frac{\log _{a b} b}{1} \\ & =\log _{a b} a+\log _{a b} b \\ & =\log _{a b}(a \times b) \\ & =\log _{a b} a b \\ & =1 \end{aligned} $$