Question 6 (6 marks):
Diagram 4 shows a cylindrical container with the length of 20 cm placed on the floor against the wall. W is the point on the edge of the base of the container. It is given that the distance of point W is 2 cm from the wall and 1 cm from the floor.
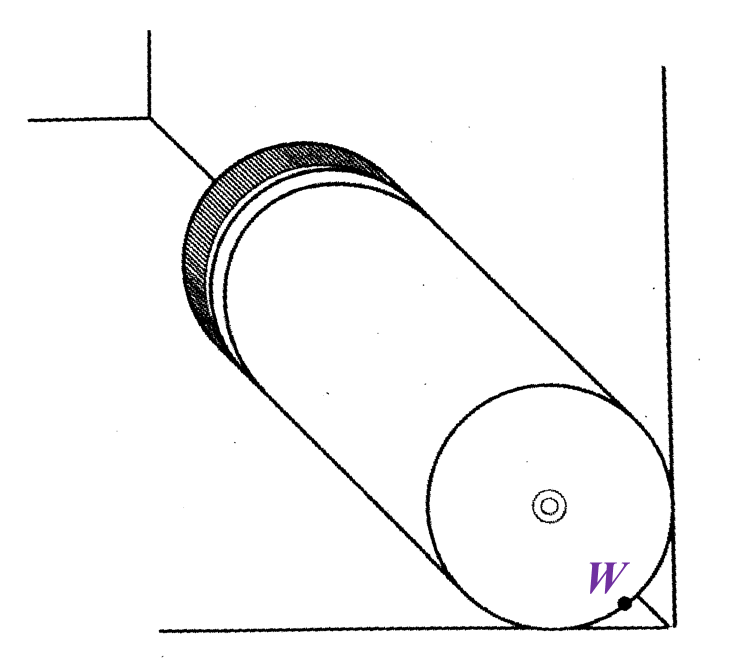
Karen wants to keep the container in a box with a dimension of 21 cm × 7 cm × 7 cm.
Determine whether the container can be kept in that box or otherwise. Give a reason for your answer.
Solution:

Diagram 4 shows a cylindrical container with the length of 20 cm placed on the floor against the wall. W is the point on the edge of the base of the container. It is given that the distance of point W is 2 cm from the wall and 1 cm from the floor.

Karen wants to keep the container in a box with a dimension of 21 cm × 7 cm × 7 cm.
Determine whether the container can be kept in that box or otherwise. Give a reason for your answer.
Solution:

Question 7 (10 marks):
(a) The mass of honeydews produced in a plantation is normally distributed with a mean of 0.8 kg and a standard deviation of 0.25 kg. The honeydews are being classified into three grades A, B and C according to their masses:
Grade A > Grade B > Grade C
(i) The minimum mass of a grade A honeydew is 1.2 kg.
If a honeydew is picked at random from the plantation, find the probability that the honeydew is of grade A.
(ii) Find the minimum mass, in kg, of grade B honeydew if 20% of the honeydews are of grade C.
(b) At the Shoot the Duck game booth at an amusement park, the probability of winning is 25%.
Jacky bought tickets to play n games. The probability for Jacky to win once is 10 times the probability of losing all games.
(i) Find the value of n.
(ii) Calculate the standard deviation of the number of wins.
Solution:
μ = 0.8 kg, σ = 0.25 kg
(a)(i)
(a)(ii)
(b)
(b)(i)
(b)(ii)
(a) The mass of honeydews produced in a plantation is normally distributed with a mean of 0.8 kg and a standard deviation of 0.25 kg. The honeydews are being classified into three grades A, B and C according to their masses:
Grade A > Grade B > Grade C
(i) The minimum mass of a grade A honeydew is 1.2 kg.
If a honeydew is picked at random from the plantation, find the probability that the honeydew is of grade A.
(ii) Find the minimum mass, in kg, of grade B honeydew if 20% of the honeydews are of grade C.
(b) At the Shoot the Duck game booth at an amusement park, the probability of winning is 25%.
Jacky bought tickets to play n games. The probability for Jacky to win once is 10 times the probability of losing all games.
(i) Find the value of n.
(ii) Calculate the standard deviation of the number of wins.
Solution:
μ = 0.8 kg, σ = 0.25 kg
(a)(i)
(a)(ii)
(b)
(b)(i)
(b)(ii)