Question 9:
In diagram 5, AOBDE, is a semicircle with centre O and has radius of 5cm. ABC is a right angle triangle.
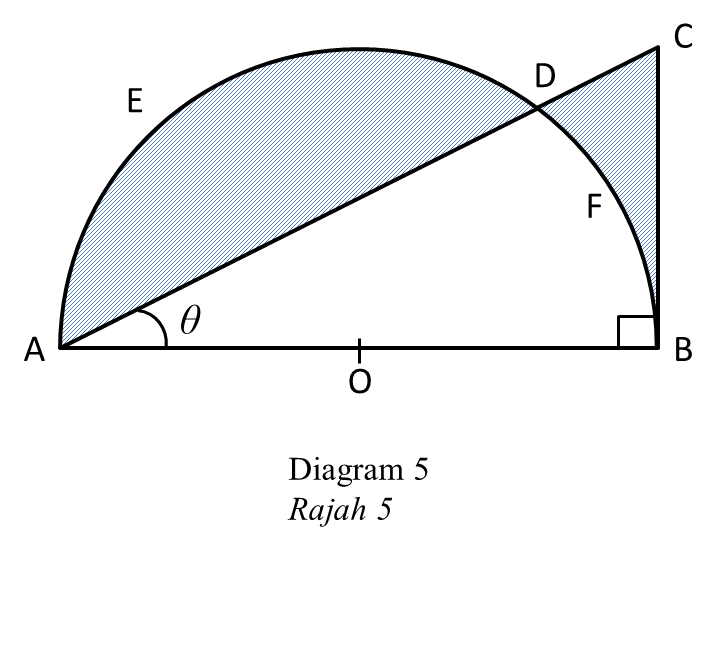
It is given that ADDC=3.85 and DC=2.31 cm.
[Use π = 3.142]
Calculate
(a) the value of θ, in radians, [2 marks]
(b) the perimeter, in cm, of the segment ADE, [3 marks]
(c) the area, in cm2, of the shaded region BCDF. [5 marks]Solution:
(a)
Given ADDC=3.85 and DC=2.31 cmAD=3.85×2.31=8.8935∴AC=8.8935+2.31=11.2035 cmcosθ=ABAC=1011.2035θ=26.80oθ=26.80o×π180o=0.4678 rad
(b)
∠AOD = 3.142 – (0.4678 × 2)
= 2.206 rad
Length of arc AED = 5 × 2.206
= 11.03 cm
Therefore, perimeter of the segment ADE
= 11.03 + 8.8935
= 19.924 cm
(c)
BC = √ AC2 – AB2
= √11.20352 – 102
= 5.052 cm
2.206 rad×180oπ=126.38o∠BOD=3.142−2.206=0.936 radArea of shaded region BCDF=Area of △ ABC−Area of △ AOD−Area of segment OBD=12(10)(5.052)−12(5)(5)(sin126.38)−12(5)2(0.936)=25.26−10.06−11.7=3.50 cm2
2.206 rad×180oπ=126.38o∠BOD=3.142−2.206=0.936 radArea of shaded region BCDF=Area of △ ABC−Area of △ AOD−Area of segment OBD=12(10)(5.052)−12(5)(5)(sin126.38)−12(5)2(0.936)=25.26−10.06−11.7=3.50 cm2