Question 9:
Solution:
(a)
(b)
(c)
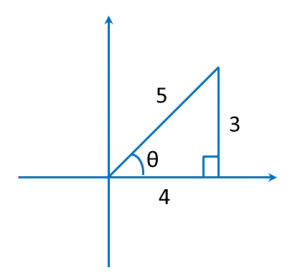
Given that sin θ =
, where θ is an acute angle, without using tables or a calculator, find the values of
(a) sin (180º + θ),
(b) cos (180º – θ),
(c) tan (360º + θ).
Solution:
(a)

sin (180º + θ)
= sin 180º cos θ + cos 180º sin θ
= (0) cos θ + (– 1) sin θ
= – sin θ
=
(b)
cos (180º – θ)
= cos 180º cos θ + sin 180º sin θ
= (– 1) cos θ + (0) sin θ
= – cos θ
=
(c)
Question 10:
Prove each of the following trigonometric identities.
(a) cot2 x – cot2 x cos2x = cos2 x
Solution:
(a)
(b)