2.9 Small Changes and Approximations - SPM Additional Mathematics

2.9 Small Changes and Approximations

$If δ x is very small, \frac{δ y}{δ x} will be a good approximation of \frac{d y}{d x},$ ,

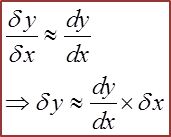
This is very useful information in determining an approximation of the change in one variable given the small change in the second variable.

Example:

Given that y = 3x² + 2x – 4. Use differentiation to find the small change in y when x increases from 2 to 2.02.

Solution:

$\begin{array}{l} y = 3 x^{2} + 2 x - 4 \\ \frac{d y}{d x} = 6 x + 2 \end{array}$

The small change in y is denoted by δy while the small change in the second quantity that can be seen in the question is the x and is denoted by δx.

$\begin{array}{l} \frac{δ y}{δ x} \approx \frac{d y}{d x} \\ δ y = \frac{d y}{d x} \times δ x \\ δ y = (6 x + 2) \times (2.02 - 2) \to δ x = new x - original x \\ δ y = [6 (2) + 2] \times 0.02 \\ Substitute x with the original value of x, i .e . 2. \\ δ y = 0.28 \end{array}$

Leave a Comment Cancel reply