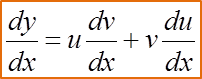2.3 First Derivatives of the Product of Two Polynomials

2.3 Find the Derivatives of a Product using Product Rule

(A) The Product Rule

Method 1

If u(x) and v(x) are two functions of x and y = uv then

Example:

Method 2 (Differentiate Directly)

Example:

$Given that y = (2 x + 3) (3 x^{3} - 2 x^{2} - x), find \frac{d y}{d x}$

Solution:

$\begin{array}{l} y = (2 x + 3) (3 x^{3} - 2 x^{2} - x) \\ \frac{d y}{d x} = (2 x + 3) (9 x^{2} - 4 x - 1) + (3 x^{3} - 2 x^{2} - x) (2) \\ \frac{d y}{d x} = (2 x + 3) (9 x^{2} - 4 x - 1) + (6 x^{3} - 4 x^{2} - 2 x) \end{array}$

Practice 1:

Given that y = 4x³(3x + 1)⁵, find dy/dx.

Solution:
y = 4x³(3x + 1)⁵
dy/dx

= 4x³. 5(3x + 1)⁴.3 + (3x + 1)⁵.12x²

= 60x³(3x + 1)⁴ + 12x²(3x + 1)⁵

= 12x²(3x + 1)⁴ [5x+ (3x+ 1)]

= 12x²(3x + 1)⁴ (8x+ 1)

Leave a Comment Cancel reply