Question 12:
Solutions by scale drawing is not accepted.
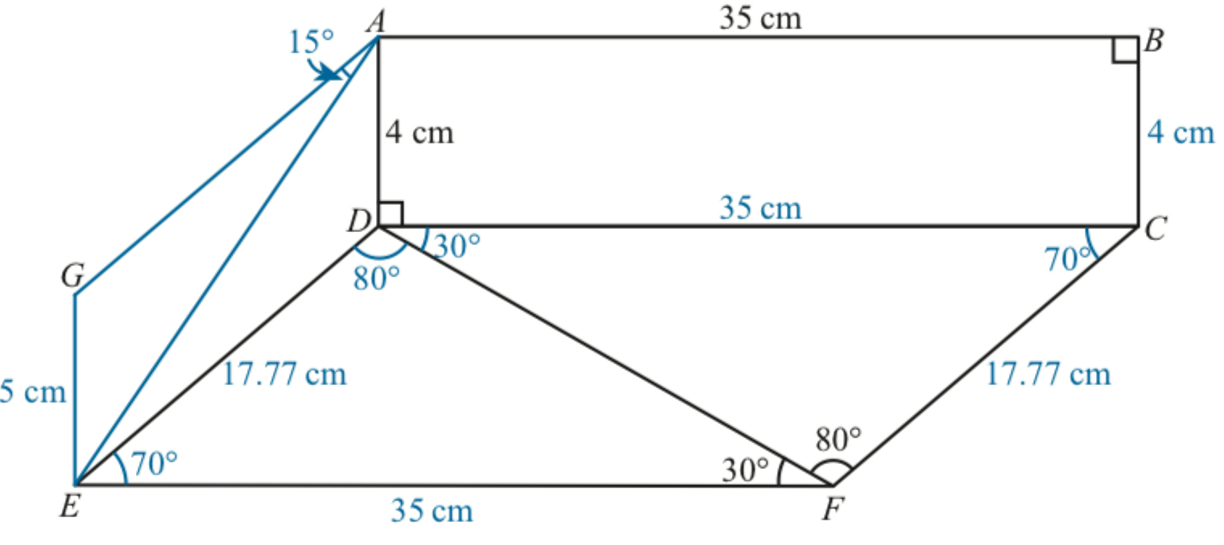
Diagram 6 shows a model. The model consists of a vertical wall ABCD and a horizontal floor CDEF. CDEF is a parallelogram.

(a) Calculate
(i) the length, in cm , of CF,
(ii) the area, in cm2, of Δ ACE.
[6 marks]
(b) A pole has a length of 5 cm . It is placed obliquely at corner E. A stick is used to join the top of the pole, G, to corner A, such that ∠EAG = 15o.
Find the minimum length, in cm, of the stick.
[4 marks]
Answer:
(a)
(i)
$$ \begin{aligned} \frac{C F}{\sin 30^{\circ}} & =\frac{35}{\sin 80^{\circ}} \\ C F & =\frac{35 \sin 30^{\circ}}{\sin 80^{\circ}} \\ C F & =17.77 \mathrm{~cm} \end{aligned} $$
(ii)
$$ \begin{aligned} & A C=\sqrt{35^2+4^2} \\ & A C=35.23 \mathrm{~cm} \end{aligned} $$
$$ \begin{aligned} & C E^2=35^2+17.77^2-2(35)(17.77) \cos 110^{\circ} \\ & C E=\sqrt{1966.2118} \\ & C E=44.34 \mathrm{~cm} \end{aligned} $$
$$ \begin{aligned} & A E^2=4^2+17.77^2-2(4)(17.77) \cos 90^{\circ} \\ & A E=\sqrt{331.7729} \\ & A E=18.21 \mathrm{~cm} \end{aligned} $$
$$ \begin{aligned} s & =\frac{35.23+44.34+18.21}{2} \\ & =48.89 \end{aligned} $$
$$ \begin{aligned} &\text { Area of } \triangle A C E\\ &\begin{aligned} & =\sqrt{s(s-a)(s-b)(s-c)} \\ & =\sqrt{48.89(48.89-35.23)(48.89-44.34)(48.89-18.21)} \\ & =305.33 \mathrm{~cm}^2 \end{aligned} \end{aligned} $$
(b)
$$ \begin{aligned} \frac{\sin \angle A G E}{18.21} & =\frac{\sin 15^{\circ}}{5} \\ \sin \angle A G E & =0.9426 \\ \angle A G E & =\sin ^{-1}(0.9426) \quad \angle A G E=70.49^{\circ} \end{aligned} $$
$$ \begin{aligned} \angle G E A & =180^{\circ}-15^{\circ}-70.49^{\circ} \\ & =94.51^{\circ} \end{aligned} $$
$$ \begin{aligned} \frac{A G}{\sin 94.51^{\circ}} & =\frac{5}{\sin 15^{\circ}} \\ A G & =\frac{5 \sin 94.51^{\circ}}{\sin 15^{\circ}} \\ A G & =19.26 \mathrm{~cm} \end{aligned} $$
Solutions by scale drawing is not accepted.
Diagram 6 shows a model. The model consists of a vertical wall ABCD and a horizontal floor CDEF. CDEF is a parallelogram.

(a) Calculate
(i) the length, in cm , of CF,
(ii) the area, in cm2, of Δ ACE.
[6 marks]
(b) A pole has a length of 5 cm . It is placed obliquely at corner E. A stick is used to join the top of the pole, G, to corner A, such that ∠EAG = 15o.
Find the minimum length, in cm, of the stick.
[4 marks]
Answer:
(a)

(i)
$$ \begin{aligned} \frac{C F}{\sin 30^{\circ}} & =\frac{35}{\sin 80^{\circ}} \\ C F & =\frac{35 \sin 30^{\circ}}{\sin 80^{\circ}} \\ C F & =17.77 \mathrm{~cm} \end{aligned} $$
(ii)
$$ \begin{aligned} & A C=\sqrt{35^2+4^2} \\ & A C=35.23 \mathrm{~cm} \end{aligned} $$
$$ \begin{aligned} & C E^2=35^2+17.77^2-2(35)(17.77) \cos 110^{\circ} \\ & C E=\sqrt{1966.2118} \\ & C E=44.34 \mathrm{~cm} \end{aligned} $$
$$ \begin{aligned} & A E^2=4^2+17.77^2-2(4)(17.77) \cos 90^{\circ} \\ & A E=\sqrt{331.7729} \\ & A E=18.21 \mathrm{~cm} \end{aligned} $$
$$ \begin{aligned} s & =\frac{35.23+44.34+18.21}{2} \\ & =48.89 \end{aligned} $$
$$ \begin{aligned} &\text { Area of } \triangle A C E\\ &\begin{aligned} & =\sqrt{s(s-a)(s-b)(s-c)} \\ & =\sqrt{48.89(48.89-35.23)(48.89-44.34)(48.89-18.21)} \\ & =305.33 \mathrm{~cm}^2 \end{aligned} \end{aligned} $$
(b)
$$ \begin{aligned} \frac{\sin \angle A G E}{18.21} & =\frac{\sin 15^{\circ}}{5} \\ \sin \angle A G E & =0.9426 \\ \angle A G E & =\sin ^{-1}(0.9426) \quad \angle A G E=70.49^{\circ} \end{aligned} $$
$$ \begin{aligned} \angle G E A & =180^{\circ}-15^{\circ}-70.49^{\circ} \\ & =94.51^{\circ} \end{aligned} $$
$$ \begin{aligned} \frac{A G}{\sin 94.51^{\circ}} & =\frac{5}{\sin 15^{\circ}} \\ A G & =\frac{5 \sin 94.51^{\circ}}{\sin 15^{\circ}} \\ A G & =19.26 \mathrm{~cm} \end{aligned} $$