Question 14:
Diagram 11.1 shows the relation of three sets.
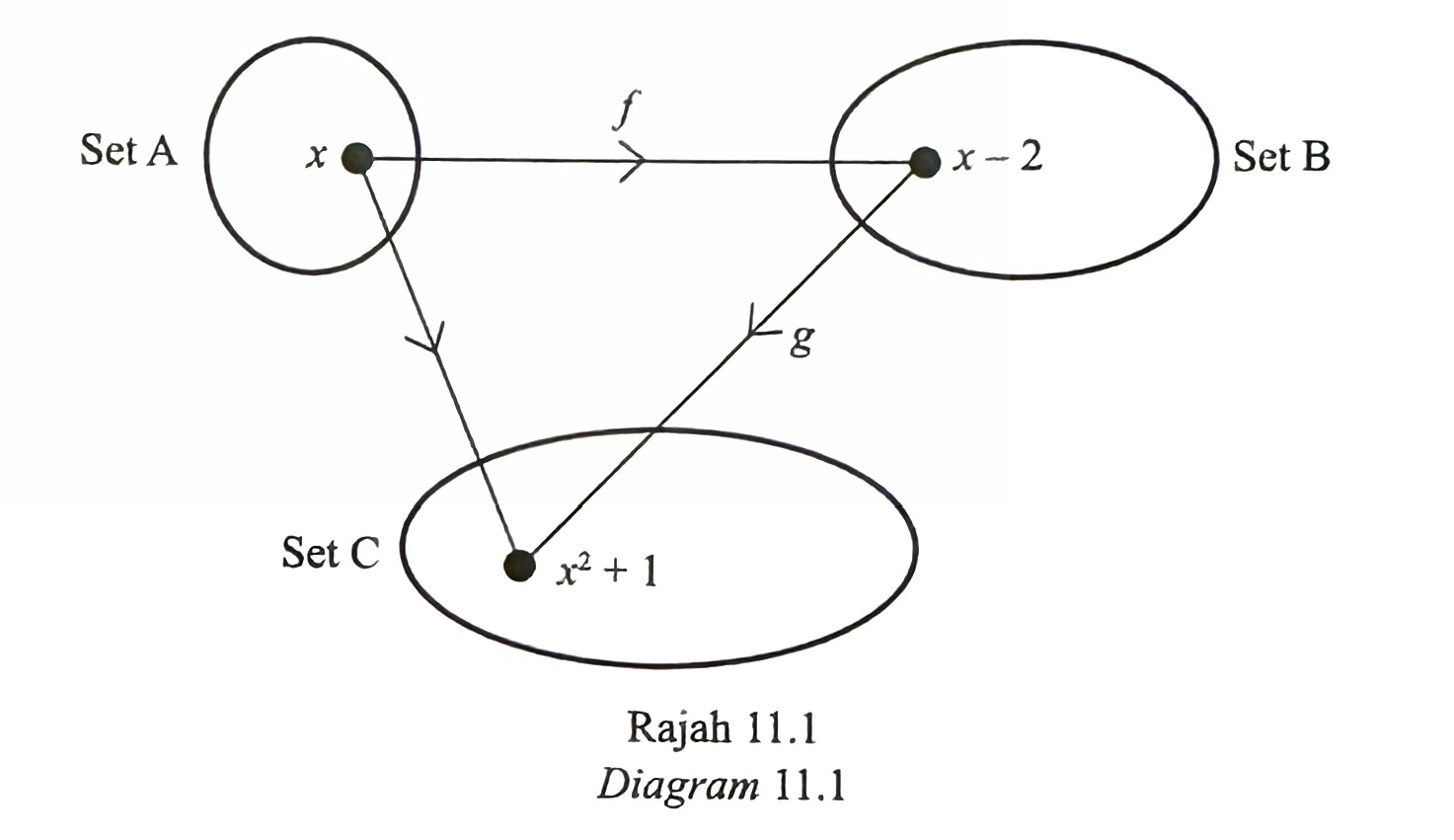(a) State gf(x).
[1 mark]
(b)(i) Determine f-1(x). Hence, find g(x).
(ii) Diagram 11.2 shows part of the graph of y = g(x).
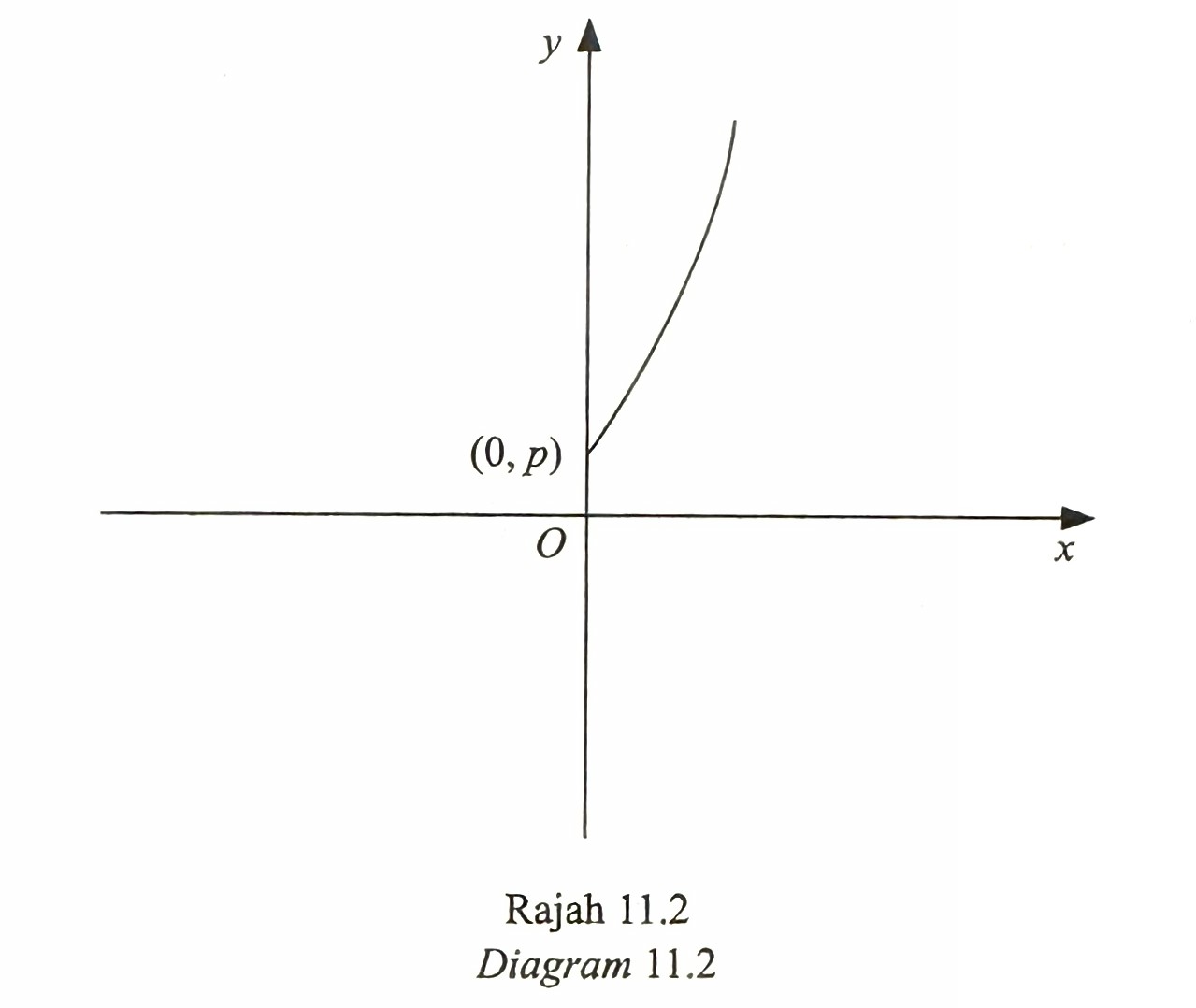Sketch the graph g-1(x) on Diagram 11.2.
[4 marks]
(c) Find f2(x), f3(x) and f4(x). Hence, state f75(x).
[3 marks]
Answer:
(a)
$$ g f(x)=x^2+1 $$
(b)(i)
$$ \begin{aligned} & f^{-1}(x-2)=x \\ & \text { Let } x-2=y \\ & x=y+2 \end{aligned} $$
$$ \begin{aligned} & f^{-1}(y)=y+2 \\ & \therefore f^{-1}(x)=x+2 \end{aligned} $$
$$ \begin{aligned} g(x) & =\left[f^{-1}(x)\right]^2+1 \\ & =(x+2)^2+1 \\ & =x^2+4 x+4+1 \\ & =x^2+4 x+5 \end{aligned} $$
(b)(ii)
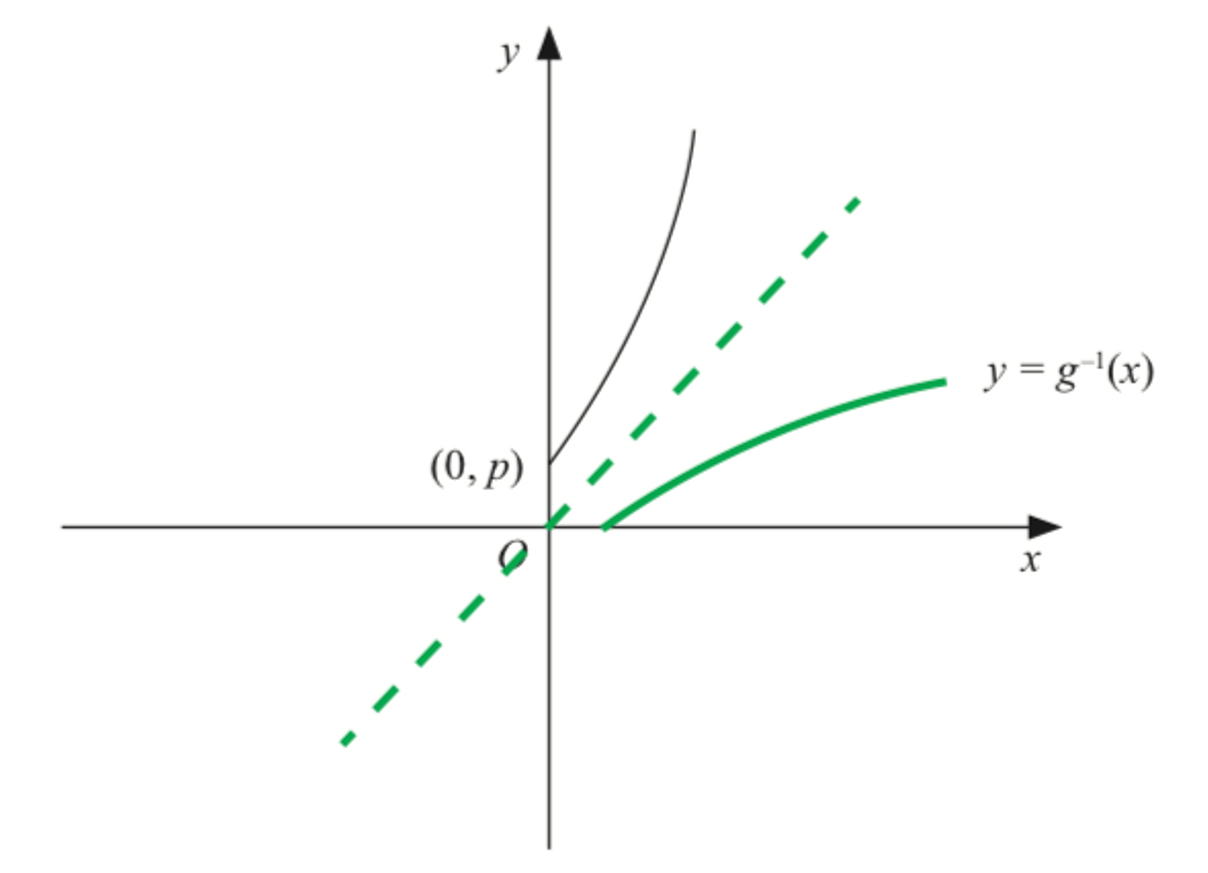
(c)
$$ \begin{aligned} & f(x)=x-2 \\ & \begin{aligned} f^2(x)=f f(x) & =f(x-2) \\ & =(x-2)-2 \\ & =x-4 \end{aligned} \end{aligned} $$
$$ \begin{aligned} f^3(x)=f f^2(x) & =f(x-4) \\ & =(x-4)-2 \\ & =x-6 \end{aligned} $$
$$ \begin{aligned} f^4(x)=f^2 f^2(x) & =f^2(x-4) \\ & =(x-4)-4 \\ & =x-8 \end{aligned} $$
$$ \begin{aligned} & f(x)=x-2(1) \\ & f^2(x)=x-2(2) \\ & f^3(x)=x-2(3) \\ & f^4(x)=x-2(4) \\ & f^n(x)=x-2(n) \end{aligned} $$
$$ \begin{aligned} \therefore f^{75}(x) & =x-2(75) \\ f^{75}(x) & =x-150 \end{aligned} $$
Diagram 11.1 shows the relation of three sets.
(a) State gf(x).[1 mark]
(b)(i) Determine f-1(x). Hence, find g(x).
(ii) Diagram 11.2 shows part of the graph of y = g(x).
Sketch the graph g-1(x) on Diagram 11.2.[4 marks]
(c) Find f2(x), f3(x) and f4(x). Hence, state f75(x).
[3 marks]
Answer:
(a)
$$ g f(x)=x^2+1 $$
(b)(i)
$$ \begin{aligned} & f^{-1}(x-2)=x \\ & \text { Let } x-2=y \\ & x=y+2 \end{aligned} $$
$$ \begin{aligned} & f^{-1}(y)=y+2 \\ & \therefore f^{-1}(x)=x+2 \end{aligned} $$
$$ \begin{aligned} g(x) & =\left[f^{-1}(x)\right]^2+1 \\ & =(x+2)^2+1 \\ & =x^2+4 x+4+1 \\ & =x^2+4 x+5 \end{aligned} $$
(b)(ii)
(c)
$$ \begin{aligned} & f(x)=x-2 \\ & \begin{aligned} f^2(x)=f f(x) & =f(x-2) \\ & =(x-2)-2 \\ & =x-4 \end{aligned} \end{aligned} $$
$$ \begin{aligned} f^3(x)=f f^2(x) & =f(x-4) \\ & =(x-4)-2 \\ & =x-6 \end{aligned} $$
$$ \begin{aligned} f^4(x)=f^2 f^2(x) & =f^2(x-4) \\ & =(x-4)-4 \\ & =x-8 \end{aligned} $$
$$ \begin{aligned} & f(x)=x-2(1) \\ & f^2(x)=x-2(2) \\ & f^3(x)=x-2(3) \\ & f^4(x)=x-2(4) \\ & f^n(x)=x-2(n) \end{aligned} $$
$$ \begin{aligned} \therefore f^{75}(x) & =x-2(75) \\ f^{75}(x) & =x-150 \end{aligned} $$