Question 11:
(a) There are (n + 1) points on the circumference of a circle. If each point is connected by a straight line to all of the other points, there are 4n straight lines formed.
Polygons can be formed by connecting points on the circumference of the circle.
Find the total number of polygons that are possible.
[4 marks]
(b) A dormitory consists of 5 bunk beds. Each bunk bed has a top bed and a bottom bed. Table 1 shows the weights of 10 boys to be placed in the dormitory. Students A and B are twins.
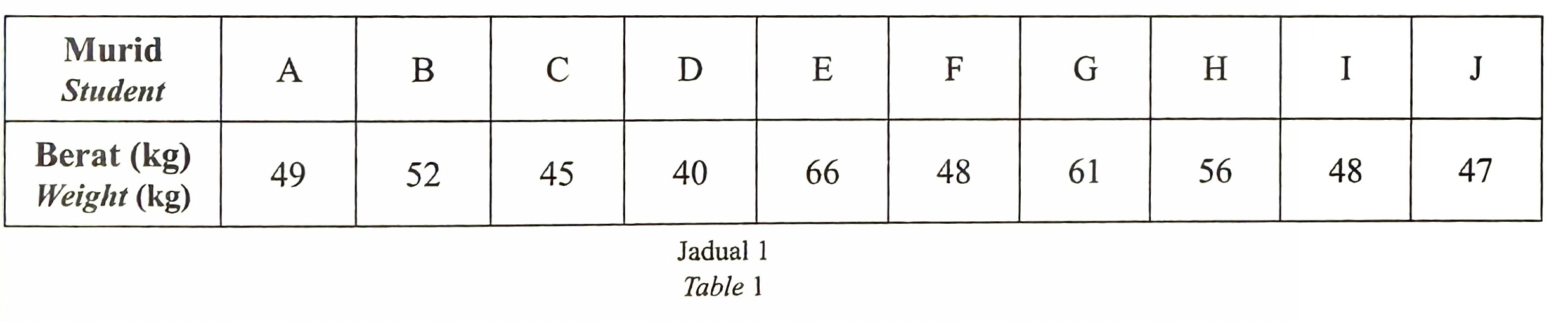
Find the number of different ways to arrange if
(i) there is no restriction,
(ii) students who weigh more than 50 kg are placed in a bottom bed and the twins are placed in the same bunk bed.
[4 marks]
Answer:
(a)
$$ \begin{aligned} { }^{n+1} C_2 & =4 n \\ \frac{(n+1)!}{2![(n+1)-2]!} & =4 n \\ \frac{(n+1)!}{2!(n-1)!} & =4 n \\ \frac{(n+1)(n)(n-1)!}{2!(n-1)!} & =4 n \\ \frac{n(n+1)}{2} & =4 n \\ n^2+n & =8 n \\ n^2+n-8 n & =0 \\ n^2-7 n & =0 \\ n(n-7) & =0 \\ n=0 \quad ; \quad n-7 & =0 \\ n & =7 \\ \therefore n=7 \quad & \end{aligned} $$
$$ \begin{aligned} &\text { Total number of polygons }\\ &\begin{aligned} & ={ }^7 C_3+{ }^7 C_4+{ }^7 C_5+{ }^7 C_6+{ }^7 C_7 \\ & =35+35+21+7+1 \\ & =99 \end{aligned} \end{aligned} $$
(b)(i)
$$ \begin{aligned} \text { Number of ways } & ={ }^{10} P_{10} \\ & =3628800 \end{aligned} $$
(b)(ii)
$$ \begin{aligned} & >50 \rightarrow B, E, G, H \\ & <50 \rightarrow A, C, D, F, I, J \end{aligned} $$
$$ \begin{aligned} \text { Number of ways } & ={ }^5 P_1 \times{ }^4 P_3 \times{ }^5 P_5 \\ & =5 \times 24 \times 120 \\ & =14400 \end{aligned} $$
(a) There are (n + 1) points on the circumference of a circle. If each point is connected by a straight line to all of the other points, there are 4n straight lines formed.
Polygons can be formed by connecting points on the circumference of the circle.
Find the total number of polygons that are possible.
[4 marks]
(b) A dormitory consists of 5 bunk beds. Each bunk bed has a top bed and a bottom bed. Table 1 shows the weights of 10 boys to be placed in the dormitory. Students A and B are twins.

Find the number of different ways to arrange if
(i) there is no restriction,
(ii) students who weigh more than 50 kg are placed in a bottom bed and the twins are placed in the same bunk bed.
[4 marks]
Answer:
(a)
$$ \begin{aligned} { }^{n+1} C_2 & =4 n \\ \frac{(n+1)!}{2![(n+1)-2]!} & =4 n \\ \frac{(n+1)!}{2!(n-1)!} & =4 n \\ \frac{(n+1)(n)(n-1)!}{2!(n-1)!} & =4 n \\ \frac{n(n+1)}{2} & =4 n \\ n^2+n & =8 n \\ n^2+n-8 n & =0 \\ n^2-7 n & =0 \\ n(n-7) & =0 \\ n=0 \quad ; \quad n-7 & =0 \\ n & =7 \\ \therefore n=7 \quad & \end{aligned} $$
$$ \begin{aligned} &\text { Total number of polygons }\\ &\begin{aligned} & ={ }^7 C_3+{ }^7 C_4+{ }^7 C_5+{ }^7 C_6+{ }^7 C_7 \\ & =35+35+21+7+1 \\ & =99 \end{aligned} \end{aligned} $$
(b)(i)
$$ \begin{aligned} \text { Number of ways } & ={ }^{10} P_{10} \\ & =3628800 \end{aligned} $$
(b)(ii)
$$ \begin{aligned} & >50 \rightarrow B, E, G, H \\ & <50 \rightarrow A, C, D, F, I, J \end{aligned} $$
$$ \begin{aligned} \text { Number of ways } & ={ }^5 P_1 \times{ }^4 P_3 \times{ }^5 P_5 \\ & =5 \times 24 \times 120 \\ & =14400 \end{aligned} $$
Question 12:
Diagram 9 shows six letter cards used in a Binomial experiment.

A card will be chosen randomly in each Bernoulli trial. The card is then replaced.
(a) If there are 120 trials, find the expected value of the number of consonant letter cards that will be chosen. [2 marks]
(b) If there are 5 trials, find the probability that the number of consonant letter cards chosen is more than the number of vowel letter cards chosen. [4 marks]
Answer:
(a)
$$ \begin{aligned} & \text { Consonant } =C, R, D, K \\ & \text { Vowel }=E, I \end{aligned} $$
$$ \begin{aligned} P(\text { Consonant } ) & =\frac{4}{6} \\ & =\frac{2}{3} \end{aligned} $$
$$ \begin{aligned} \text { Expected value } & =(120)\left(\frac{2}{3}\right) \\ & =80 \end{aligned} $$
(b)
$$ \begin{aligned} & \text { Let } X=\text { Consonant } \\ & \begin{aligned} P(X>2) & =P(X=3)+P(X=4)+P(X=5) \\ & ={ }^5 C_3\left(\frac{2}{3}\right)^3\left(\frac{1}{3}\right)^2+{ }^5 C_4\left(\frac{2}{3}\right)^4\left(\frac{1}{3}\right)^1+{ }^5 C_5\left(\frac{2}{3}\right)^5\left(\frac{1}{3}\right)^0 \\ & =0.3292+0.3292+0.1317 \\ & =0.7901 \end{aligned} \end{aligned} $$
Diagram 9 shows six letter cards used in a Binomial experiment.

A card will be chosen randomly in each Bernoulli trial. The card is then replaced.
(a) If there are 120 trials, find the expected value of the number of consonant letter cards that will be chosen. [2 marks]
(b) If there are 5 trials, find the probability that the number of consonant letter cards chosen is more than the number of vowel letter cards chosen. [4 marks]
Answer:
(a)
$$ \begin{aligned} & \text { Consonant } =C, R, D, K \\ & \text { Vowel }=E, I \end{aligned} $$
$$ \begin{aligned} P(\text { Consonant } ) & =\frac{4}{6} \\ & =\frac{2}{3} \end{aligned} $$
$$ \begin{aligned} \text { Expected value } & =(120)\left(\frac{2}{3}\right) \\ & =80 \end{aligned} $$
(b)
$$ \begin{aligned} & \text { Let } X=\text { Consonant } \\ & \begin{aligned} P(X>2) & =P(X=3)+P(X=4)+P(X=5) \\ & ={ }^5 C_3\left(\frac{2}{3}\right)^3\left(\frac{1}{3}\right)^2+{ }^5 C_4\left(\frac{2}{3}\right)^4\left(\frac{1}{3}\right)^1+{ }^5 C_5\left(\frac{2}{3}\right)^5\left(\frac{1}{3}\right)^0 \\ & =0.3292+0.3292+0.1317 \\ & =0.7901 \end{aligned} \end{aligned} $$