Question 10:
(a)
$$ \text { Given that } \frac{\mathrm{d}}{\mathrm{~d} x}\left(\frac{1}{x^2+1}\right)=g(x), \text { find } \int[3 g(x)+1] \mathrm{d} x . $$
[3 marks]
(b)
$$ \text { Diagram } 8 \text { shows the graph } x=f(y) \text {. } $$
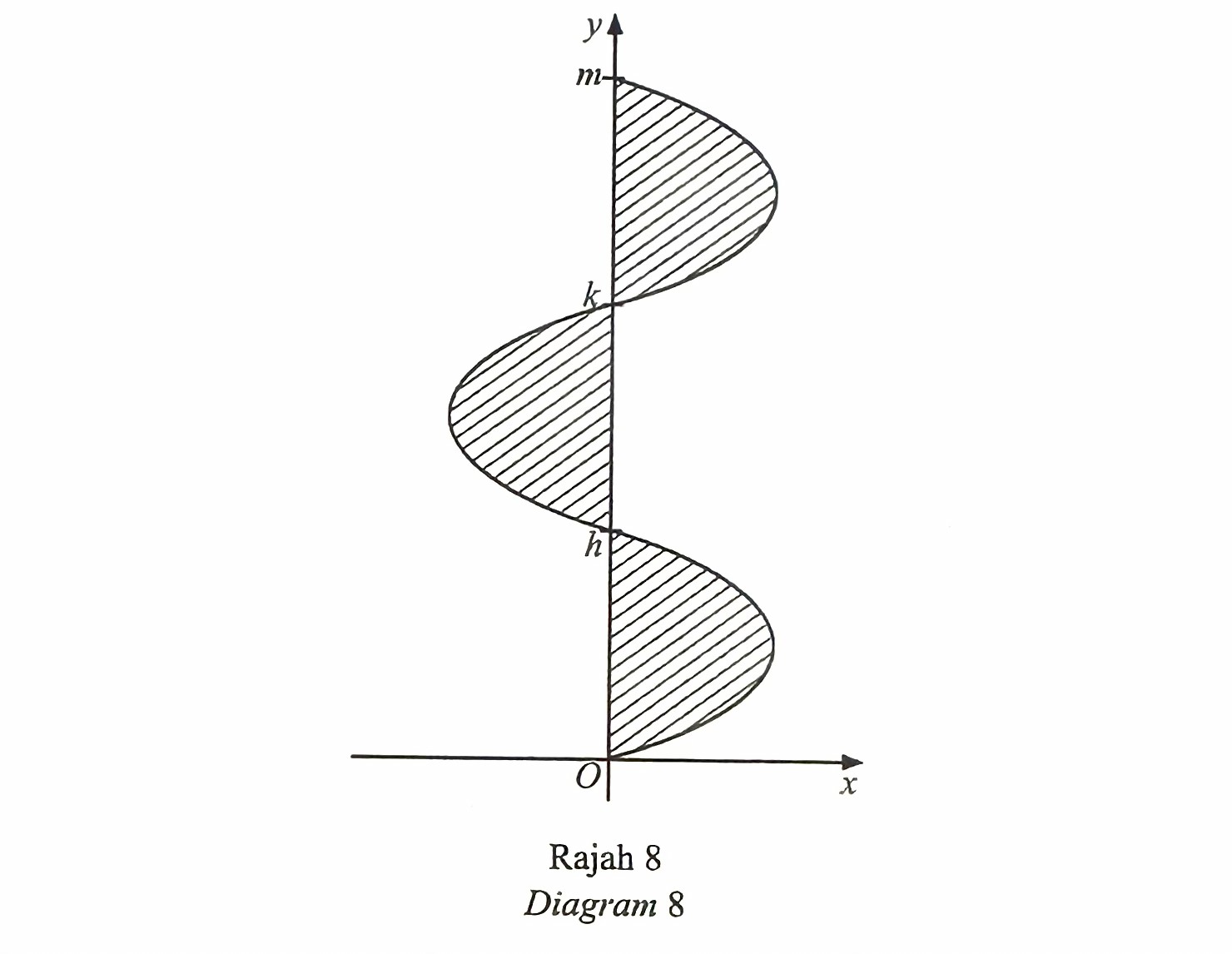
$$ \text { It is given that area of the shaded region is } \frac{9}{2} \text { unit }^2 \text { and } \int_0^h f(y) \mathrm{d} y=\int_k^m f(y) \mathrm{d} y=\frac{3}{2} \text {. } $$
find the value of
(i)
$$ \int_0^k f(y) \mathrm{d} y, $$
(ii)
$$ \int_h^k x \mathrm{~d} y+\int_k^m \frac{5}{4} f(y) \mathrm{d} y $$
[3 marks]
Answer:
(a)
$$ \begin{aligned} \int[3 g(x)+1] \mathrm{d} x & =3\left(\frac{1}{x^2+1}\right)+\int 1 \mathrm{~d} x \\ & =\frac{3}{x^2+1}+x+c \end{aligned} $$
(b)(i)
$$ \begin{aligned} \int_0^h f(y) \mathrm{d} y+\left|\int_h^k f(y) \mathrm{d} y\right|+\int_k^m f(y) \mathrm{d} y & =\frac{9}{2} \\ \frac{3}{2}+\left|\int_h^k f(y) \mathrm{d} y\right|+\frac{3}{2} & =\frac{9}{2} \\ \left|\int_h^k f(y) \mathrm{d} y\right| & =\frac{9}{2}-\frac{3}{2}-\frac{3}{2} \\ \left|\int_h^k f(y) \mathrm{d} y\right| & =\frac{3}{2} \\ \int_h^k f(y) \mathrm{d} y & =-\frac{3}{2} \end{aligned} $$
$$ \begin{aligned} \int_0^k f(y) \mathrm{d} y & =\int_0^h f(y) \mathrm{d} y+\int_h^k f(y) \mathrm{d} y \\ & =\frac{3}{2}+\left(-\frac{3}{2}\right) \\ & =0 \end{aligned} $$
(b)(ii)
$$ \begin{aligned} \int_h^k x \mathrm{~d} y+\int_k^m \frac{5}{4} f(y) \mathrm{d} y & =\int_h^k f(y) \mathrm{d} y+\frac{5}{4} \int_k^m f(y) \mathrm{d} y \\ & =-\frac{3}{2}+\frac{5}{4}\left(\frac{3}{2}\right) \\ & =-\frac{3}{2}+\frac{15}{8} \\ & =\frac{3}{8} \end{aligned} $$
(a)
$$ \text { Given that } \frac{\mathrm{d}}{\mathrm{~d} x}\left(\frac{1}{x^2+1}\right)=g(x), \text { find } \int[3 g(x)+1] \mathrm{d} x . $$
[3 marks]
(b)
$$ \text { Diagram } 8 \text { shows the graph } x=f(y) \text {. } $$

$$ \text { It is given that area of the shaded region is } \frac{9}{2} \text { unit }^2 \text { and } \int_0^h f(y) \mathrm{d} y=\int_k^m f(y) \mathrm{d} y=\frac{3}{2} \text {. } $$
find the value of
(i)
$$ \int_0^k f(y) \mathrm{d} y, $$
(ii)
$$ \int_h^k x \mathrm{~d} y+\int_k^m \frac{5}{4} f(y) \mathrm{d} y $$
[3 marks]
Answer:
(a)
$$ \begin{aligned} \int[3 g(x)+1] \mathrm{d} x & =3\left(\frac{1}{x^2+1}\right)+\int 1 \mathrm{~d} x \\ & =\frac{3}{x^2+1}+x+c \end{aligned} $$
(b)(i)
$$ \begin{aligned} \int_0^h f(y) \mathrm{d} y+\left|\int_h^k f(y) \mathrm{d} y\right|+\int_k^m f(y) \mathrm{d} y & =\frac{9}{2} \\ \frac{3}{2}+\left|\int_h^k f(y) \mathrm{d} y\right|+\frac{3}{2} & =\frac{9}{2} \\ \left|\int_h^k f(y) \mathrm{d} y\right| & =\frac{9}{2}-\frac{3}{2}-\frac{3}{2} \\ \left|\int_h^k f(y) \mathrm{d} y\right| & =\frac{3}{2} \\ \int_h^k f(y) \mathrm{d} y & =-\frac{3}{2} \end{aligned} $$
$$ \begin{aligned} \int_0^k f(y) \mathrm{d} y & =\int_0^h f(y) \mathrm{d} y+\int_h^k f(y) \mathrm{d} y \\ & =\frac{3}{2}+\left(-\frac{3}{2}\right) \\ & =0 \end{aligned} $$
(b)(ii)
$$ \begin{aligned} \int_h^k x \mathrm{~d} y+\int_k^m \frac{5}{4} f(y) \mathrm{d} y & =\int_h^k f(y) \mathrm{d} y+\frac{5}{4} \int_k^m f(y) \mathrm{d} y \\ & =-\frac{3}{2}+\frac{5}{4}\left(\frac{3}{2}\right) \\ & =-\frac{3}{2}+\frac{15}{8} \\ & =\frac{3}{8} \end{aligned} $$